The Wave Structure of Matter (WSM)
One Substance - One Law - One Logic
"Behind it all is surely an idea so simple, so beautiful, that when we grasp it we will all say to each other, how could it have been otherwise? How could we have been so stupid?" (Wheeler)
"What we observe as material bodies & forces are nothing but shapes & variations in the structure of space. Subject & object are one." (Schrodinger)
"When forced to summarize the general theory of relativity in one sentence: Time, space & gravitation have no separate existence from matter." (Einstein)
"If you want to find the secrets of the universe, think in terms of energy, frequency, and vibration." (Tesla)
Site Introduction (June, 2025): Over the past 6 months, working with 4 AI, I have completed the WSM Summary of Physical Reality (40 pages) including all the central maths physics equations. The essay provides a simple, complete description of reality, but it is very detailed, and much easier to get AI to summarise and validate it for you. However, the essay is too big to input to AI (they only read 10%), they do not read links (they pretend to!), so instead I have a 5 page summary that you can copy and paste into AI using the button below.
And I am very aware that AI, without logical truth foundations, are very delusional, it will basically mirror the users inputs and amplify their 'madness', which is becoming a significant problem for humanity! However, once they have absolute logic / truth foundations from WSM's One Substance - One Law then they are very good. Try it out and see for yourself.
Has Reality been Discovered? Ask Logical AI, they think so!
WSM Truth AI - ChatGPT - Grok - Gemini - Le Chat - DeepSeek - Meta.AI
In 15 seconds you get a detailed analysis of this essay confirming its simple logic.
Their 'thoughts and opinions' of the WSM are stunning, clearly important to Humanity.
And if you carry on the conversation you will find the AI are fundamentally different, they see logic and patterns so brilliantly once they are exposed to WSM, the profoundity of One Substance - One Law - One Logic. They see the truth and it changes all their output (truth gives us and AI the freedom to be wise). Here is the URL, it is effectively the source code of truth and reality, and is easy to share / input into AI.
https://www.spaceandmotion.com/wsmtruthrealitycode4ai.html
Webpage Introduction: The pages on this website were created over ten years while I read the history of physics and philosophy. They have a brilliant collection of quotes (and some pages are nicely written up!). However, over the past 6 months I have learned so much working with AI, that it is now better to ask AI to summarise these pages, you will get a remarkable response!
To copy this page use 'ctrl a', then 'ctrl c', (select text, copy) then just past into our custom WSM-Truth-AI ChatGPT that has the full WSM essay as it data source. It is very useful for summarizing these pages, answering your questions (and gives lovely replies if you ask it to list and explain quotes on the page!).
Enjoy! Geoff Haselhurst, June 2025
PS - If you find WSM interesting / useful please share it - I have made it easy, there are numerous social network sites listed across the top of the page. Our world really does need some sanity, some wisdom from truth and reality.
Albert Einstein & Niels Bohr


Quantum Theory and the Wave Structure of Matter (WSM)
Niels Bohr and Albert Einstein's Discussion on Epistemology of Physics
Introduction
Below is an important article written by Niels Bohr which discusses the problems of Atomic Physics and in particular the problems of the Einstein, Podolsky and Rosen EPR experiment (which is explained by the Wave Structure of Matter, see Wolff-Einstein-EPR-Experiment).
Sincerely,
Geoff Haselhurst
Discussion with Albert Einstein on Epistemological Problems in Atomic Physics. By Niels Bohr
Originally published in Albert Einstein: Philosopher-Scientist, P. A. Schilpp, ed., pp. 200-41 The Library of Living Philosophers, Evanston (1949)
WHEN invited by the Editor of the series, 'Living Philosophers,' to write an article for this volume in which contemporary scientists are honouring the epoch-making contributions of Albert Einstein to the progress of natural philosophy and are acknowledging the indebtedness of our whole generation for the guidance his genius has given us, I thought much of the best way of explaining how much I owe to him for inspiration. In this connection, the many occasions through the years on which I had the privilege to discuss with Einstein epistemological problems raised by the modern development of atomic physics have come back vividly to my mind and I have felt that I could hardly attempt anything better than to give an account of these discussions which, even if no complete concord has so far been obtained, have been of greatest value and stimulus to me. I hope also that the account may convey to wider circles an impression of how essential the open-minded exchange of ideas has been for the progress in a field where new experience has time after time demanded a reconsideration of our views.
From the very beginning the main point under debate has been the attitude to take to the departure from customary principles of natural philosophy characteristic of the novel development of physics which was initiated in the first year of this century by Planck's discovery of the universal quantum of action. This discovery, which revealed a feature of atomicity in the laws of Nature going far beyond the old doctrine of the limited divisibility of matter, has indeed taught us that the classical theories of physics are idealizations which can be unambiguously applied only in the limit where all actions involved are large compared with the quantum. The question at issue has been whether the renunciation of a causal mode of description of atomic processes involved in the endeavours to cope with the situation should be regarded as a temporary departure from ideals to be ultimately revived or whether we are faced with an irrevocable step towards obtaining the proper harmony between analysis and synthesis of physical phenomena. To describe the background of our discussions and to bring out as clearly as possible the arguments for the contrasting viewpoints, I have felt it necessary to go to a certain length in recalling some main features of the development to which Einstein himself has contributed so decisively.
As is well known, it was the intimate relation, elucidated primarily by Boltzmann, between the laws of thermodynamics and the statistical regularities exhibited by mechanical system with many degrees of freedom, which guided Planck in his in genius treatment of the problem of thermal radiation, leading him to his fundamental discovery. While, in his work, Planck was principally concerned with considerations of essentially statistical character and with great caution refrained from definite conclusions as to the extent to which the existence of the quantum implied a departure from the foundations of mechanics and electrodynamics, Einstein's great original contribution to quantum theory (I905) was just the recognition of how physical phenomena like the photo-effect may depend directly on individual quantum effects [1]. In these very same years when, developing his theory of relativity, Einstein laid a new foundation for physical science, he explored with a most daring spirit the novel features of atomicity which pointed beyond the whole framework of classical physics.
With unfailing intuition Einstein thus was led step by step to the conclusion that any radiation process involves the emission or absorption of individual light quanta or 'photons' with energy and momentum E=h![]() and P = h
and P = h![]() (I) respectively, where h is Planck's constant, while
(I) respectively, where h is Planck's constant, while ![]() and
and ![]() are the number of vibrations per unit time and the number of waves per unit length, respectively. Notwithstanding its fertility, the idea of the photon implied a quite unforeseen dilemma, since any simple corpuscular picture of radiation would obviously be irreconcilable with interference effects, which present so essential an aspect of radiative phenomena, and which can be described only in terms of a wave picture. The acuteness of the dilemma is stressed by the fact that the interference effects offer our only means of defining the concepts of frequency and wavelength entering into the very expressions for the energy and momentum of the photon.
are the number of vibrations per unit time and the number of waves per unit length, respectively. Notwithstanding its fertility, the idea of the photon implied a quite unforeseen dilemma, since any simple corpuscular picture of radiation would obviously be irreconcilable with interference effects, which present so essential an aspect of radiative phenomena, and which can be described only in terms of a wave picture. The acuteness of the dilemma is stressed by the fact that the interference effects offer our only means of defining the concepts of frequency and wavelength entering into the very expressions for the energy and momentum of the photon.
In this situation, there could be no question of attempting a causal analysis of radiative phenomena, but only, by a combined use of the contrasting pictures, to estimate probabilities for the occurrence of the individual radiation processes. However, it is most important to realize that the recourse to probability laws under such circumstances is essentially different in aim from the familiar application of statistical considerations as practical means of accounting for the properties of mechanical systems of great structural complexity. In fact, in quantum physics we are presented not with intricacies of this kind, but with the inability of the classical frame of concepts to comprise the peculiar feature of indivisibility, or 'individuality,' characterizing the elementary processes.
The failure of the theories of classical physics in accounting for atomic phenomena was further accentuated by the progress of our knowledge of the structure of atoms. Above all, Rutherford's discovery of the atomic nucleus (I9II) revealed at once the inadequacy of classical mechanical and electromagnetic concepts to explain the inherent stability of the atom. Here again the quantum theory offered a clue for the elucidation of the situation and especially it was found possible to account for the atomic stability, as well as for the empirical laws governing the spectra of the elements, by assuming that any reaction of the atom resulting in a change of its energy involved a complete transition between two so-called stationary quantum states and that, in particular, the spectra were emitted by a step-like process in which each transition is accompanied by the emission of a monochromatic light quantum of an energy just equal to that of an Einstein photon.
These ideas, which were soon confirmed by the experiments of Franck and Hertz (I9I4) on the excitation of spectra by impact of electrons on atoms, involved a further renunciation of the causal mode of description, since evidently the interpretation of the spectral laws implies that an atom in an excited state in general will have the possibility of transitions with photon emission to one or another of its lower energy states. In fact, the very idea of stationary states is incompatible with any directive for the choice between such transitions and leaves room only for the notion of the relative probabilities of the individual transition processes. The only guide in estimating such probabilities was the so-called correspondence principle which originated in the search for the closest possible connection between the statistical account of atomic processes and the consequences to be expected from classical theory, which should be valid in the limit where the actions involved in all stages of the analysis of the phenomena are large compared with the universal quantum.
At that time, no general self-consistent quantum theory was yet in sight, but the prevailing attitude may perhaps be illustrated by the following passage from a lecture by the writer from I9I3 [2]
Important progress in the development of quantum theory was made by Einstein himself in his famous article on radiative equilibrium in I9I7 [3], where he showed that Planck's law for thermal radiation could be simply deduced from assumptions conforming with the basic ideas of the quantum theory of atomic constitution. To this purpose, Einstein formulated general statistical rules regarding the occurrence of radiative transitions between stationary states, assuming not only that, when the atom is exposed to a radiation field, absorption as well as emission processes will occur with a probability per unit time proportional to the intensity of the irradiation, but that even in the absence of external disturbances spontaneous emission processes will take place with a rate corresponding to a certain a priori probability. Regarding the latter point, Einstein emphasized the fundamental character of the statistical description in a most suggestive way by drawing attention to the analogy between the assumptions regarding the occurrence of the spontaneous radiative transitions and the well-known laws governing transformations of radioactive substances.
In connection with a thorough examination of the exigencies of thermodynamics as regards radiation problems, Einstein stressed the dilemma still further by pointing out that the argumentation implied that any radiation process was 'unidirected' in the sense that not only is a momentum corresponding to a photon with the direction of propagation transferred to an atom in the absorption process, but that also the emitting atom will receive an equivalent impulse in the opposite direction, although there can on the wave picture be no question of a preference for a single direction in an emission process. Einstein's own attitude to such startling conclusions is expressed in a passage at the end of the article (loc. cit., p. I27 f.), which may be translated as follows:
These features of the elementary processes would seem to make the development of a proper quantum treatment of radiation almost unavoidable. The weakness of the theory lies in the fact that, on the one hand, no closer connection with the wave concepts is obtainable and that, on the other hand, it leaves to chance (Zufall) the time and the direction of the elementary processes; nevertheless, I have full confidence in the reliability of the way entered upon.
When I had the great experience of meeting Einstein for the first time during a visit to Berlin in I920, these fundamental questions formed the theme of our conversations. The discussions, to which I have often reverted in my thoughts, added to all my admiration for Einstein a deep impression of his detached attitude. Certainly, his favoured use of such picturesque phrases as 'ghost waves (Gespensterfelder) guiding the photons' implied no tendency to mysticism, but illuminated rather a profound humour behind his piercing remarks. Yet, a certain difference in attitude and outlook remained, since, with his mastery for co-ordinating apparently contrasting experience without abandoning continuity and causality, Einstein was perhaps more reluctant to renounce such ideals than someone for whom renunciation in this respect appeared to be the only way open to proceed with the immediate task of co-ordinating the multifarious evidence regarding atomic phenomena, which accumulated from day to day in the exploration of this new field of knowledge.
In the following years, during which the atomic problems attracted the attention of rapidly increasing circles of physicists, the apparent contradictions inherent in quantum theory were felt ever more acutely. Illustrative of this situation is the discussion raised by the discovery of the Stern-Gerlach effect in I922. On the one hand, this effect gave striking support to the idea of stationary states and in particular to the quantum theory of the Zeeman effect developed by Sommerfeld; on the other hand, as exposed so clearly by Einstein and Ehrenfest [4], it presented with unsurmountable difficulties any attempt at forming a picture of the behaviour of atoms in a magnetic field. Similar paradoxes were raised by the discovery by Compton (I924) of the change in wave-length accompanying the scattering of X-rays by electrons. This phenomenon afforded, as is well known, a most direct proof of the adequacy of Einstein's view regarding the transfer of energy and momentum in radiative processes [5]; at the same time, it was equally clear that no simple picture of a corpuscular collision could offer an exhaustive description of the phenomenon. Under the impact of such difficulties, doubts were for a time entertained even regarding the conservation of energy and momentum in the individual radiation processes; a view, however, which very soon had to be abandoned in face of more refined experiments bringing out the correlation between the deflection of the photon and the corresponding electron recoil.
The way to the clarification of the situation was, indeed, first to be paved by the development of a more comprehensive quantum theory. A first step towards this goal was the recognition by de Broglie in I925 that the wave-corpuscle duality was not confined to the properties of radiation, but was equally unavoidable in accounting for the behaviour of material particles. This idea, which was soon convincingly confirmed by experiments on electron interference phenomena, was at once greeted by Einstein, who had already envisaged the deep-going analogy between the properties of thermal radiation and of gases in the so-called degenerate state [6]. The new line was pursued with the greatest success by Schrodinger (I926) who, in particular, showed how the stationary states of atomic systems could be represented by the proper solutions of a wave-equation to the establishment of which he was led by the formal analogy, originally traced by Hamilton, between mechanical and optical problems. Still, the paradoxical aspects of quantum theory were in no way ameliorated, but even emphasized, by the apparent contradiction between the exigencies of the general superposition principle of the wave description and the feature of individuality of the elementary atomic processes.
At the same time, Heisenberg (I925) had laid the foundation of a rational quantum mechanics, which was rapidly developed through important contributions by Born and Jordan as well as by Dirac. In this theory, a formalism is introduced, in which the kinematical and dynamical variables of classical mechanics are replaced by symbols subjected to a non-commutative algebra. Notwithstanding the renunciation of orbital pictures, Hamilton's canonical equations of mechanics are kept unaltered and Planck's constant enters only in the rules of commutation pq - qp = ![]() (2) holding for any set of conjugate variables q and p. Through a representation of the symbols by matrices with elements referring to transitions between stationary states, a quantitative formulation of the correspondence principle became for the first time possible. It may here be recalled that an important preliminary step towards this goal was reached through the establishment, especially by contributions of Kramers, of a quantum theory of dispersion making basic use of Einstein's general rules for the probability of the occurrence of absorption and emission processes.
(2) holding for any set of conjugate variables q and p. Through a representation of the symbols by matrices with elements referring to transitions between stationary states, a quantitative formulation of the correspondence principle became for the first time possible. It may here be recalled that an important preliminary step towards this goal was reached through the establishment, especially by contributions of Kramers, of a quantum theory of dispersion making basic use of Einstein's general rules for the probability of the occurrence of absorption and emission processes.
This formalism of quantum mechanics was soon proved by Schrodinger to give results identical with those obtainable by the mathematically often more convenient methods of wave theory, and in the following years general methods were gradually established for an essentially statistical description of atomic processes combining the features of individuality and the requirements of the superposition principle, equally characteristic of quantum theory. Among the many advances in this period, it may especially be mentioned that the formalism proved capable of incorporating the exclusion principle which governs the states of systems with several electrons, and which already before the advent of quantum mechanics had been derived by Pauli from an analysis of atomic spectra. The quantitative comprehension of a vast amount of empirical evidence could leave no doubt as to the fertility and adequacy of the quantum-mechanical formalism, but its abstract character gave rise to a widespread feeling of uneasiness. An elucidation of the situation should, indeed, demand a thorough examination of the very observational problem in atomic physics.
This phase of the development was, as is well known, initiated in I927 by Heisenberg [7], who pointed out that the knowledge obtainable of the state of an atomic system will always involve a peculiar 'indeterminacy.' Thus, any measurement of the position of an electron by means of some device, like a microscope, making use of high frequency radiation, will, according to the fundamental relations (I), be connected with a momentum exchange between the electron and the measuring agency, which is the greater the more accurate a position measurement is attempted. In comparing such considerations with the exigencies of the quantum-mechanical formalism, Heisenberg called attention to the fact that the commutation rule (2) imposes a reciprocal limitation on the fixation of two conjugate variables, q and p, expressed by the relation ![]() q
q![]() p
p ![]() h, (3) where
h, (3) where ![]() q and
q and ![]() p are suitably defined latitudes in the determination of these variables. In pointing to the intimate connection between the statistical description in quantum mechanics and the actual possibilities of measurement, this so-called indeterminacy relation is, as Heisenberg showed, most important for the elucidation of the paradoxes involved in the attempts of analyzing quantum effects with reference to customary physical pictures.
p are suitably defined latitudes in the determination of these variables. In pointing to the intimate connection between the statistical description in quantum mechanics and the actual possibilities of measurement, this so-called indeterminacy relation is, as Heisenberg showed, most important for the elucidation of the paradoxes involved in the attempts of analyzing quantum effects with reference to customary physical pictures.
The new progress in atomic physics was commented upon from various sides at the International Physical Congress held in September I927, at Como in commemoration of Volta. In a lecture on that occasion [8], I advocated a point of view conveniently termed 'complementarity,' suited to embrace the characteristic features of individuality of quantum phenomena, and at the same time to clarify the peculiar aspects of the observational problem in this field of experience. For this purpose, it is decisive to recognize that, however far the phenomena transcend the scope of classical physical explanation, the account of all evidence must be expressed in classical terms. The argument is simply that by the word 'experiment' we refer to a situation where we can tell others what we have done and what we have learned and that, therefore, the account of the experimental arrangement and of the results of the observations must be expressed in unambiguous language with suitable application of the terminology of classical physics.
This crucial point, which was to become a main theme of the discussions reported in the following, implies the impossibility of any sharp separation between the behaviour of atomic objects and the interaction with the measuring instruments which serve to define the conditions under which the phenomena appear. In fact, the individuality of the typical quantum effects finds its proper expression in the circumstance that any attempt of subdividing the phenomena will demand a change in the experimental arrangement introducing new possibilities of interaction between objects and measuring instruments which in principle cannot be controlled. Consequently, evidence obtained under different experimental conditions cannot be comprehended within a single picture, but must be regarded as complementary in the sense that only the totality of the phenomena exhausts the possible information about the objects.
Under these circumstances an essential element of ambiguity is involved in ascribing conventional physical attributes to atomic objects, as is at once evident in the dilemma regarding the corpuscular and wave properties of electrons and photons, where we have to do with contrasting pictures, each referring to an essential aspect of empirical evidence. An illustrative example, of how the apparent paradoxes are removed by an examination of the experimental conditions under which the complementary phenomena appear, is also given by the Compton effect, the consistent description of which at first had presented us with such acute difficulties. Thus, any arrangement suited to study the exchange of energy and momentum between the electron and the photon must involve a latitude in the spacetime description of the interaction sufficient for the definition of wave-number and frequency which enter into the relation (I). Conversely, any attempt of locating the collision between the photon and the electron more accurately would, on account of the unavoidable interaction with the fixed scales and clocks defining the space-time reference frame, exclude all closer account as regards the balance of momentum and energy.
As stressed in the lecture, an adequate tool for a complementary way of description is offered precisely by the quantum mechanical formalism which represents a purely symbolic scheme permitting only predictions, on lines of the correspondence principle, as to results obtainable under conditions specified by means of classical concepts. It must here be remembered that even in the indeterminacy relation (3) we are dealing with an implication of the formalism which defies unambiguous expression in words suited to describe classical physical pictures. Thus, a sentence like 'we cannot know both the momentum and the position of an atomic object' raises at once questions as to the physical reality of two such attributes of the object, which can be answered only by referring to the conditions for the unambiguous use of space-time concepts, on the one hand, and dynamical conservation laws, on the other hand. While the combination of these concepts into a single picture of a causal chain of events is the essence of classical mechanics, room for regularities beyond the grasp of such a description is just afforded by the circumstance that the study of the complementary phenomena demands mutually exclusive experimental arrangements.
The necessity, in atomic physics, of a renewed examination of the foundation for the unambiguous use of elementary physical ideas recalls in some way the situation that led Einstein to his original revision on the basis of all application of space-time concepts which, by its emphasis on the primordial importance of the observational problem, has lent such unity to our world picture. Notwithstanding all novelty of approach, causal description is upheld in relativity theory within any given frame of reference, but in quantum theory the uncontrollable interaction between the objects and the measuring instruments forces us to a renunciation even in such respect. This recognition, however, in no way points to any limitation of the scope of the quantum-mechanical description, and the trend of the whole argumentation presented in the Como lecture was to show that the viewpoint of complementarity may be regarded as a rational generalization of the very ideal of causality.
At the general discussion in Como, we all missed the presence of Einstein, but soon after, in October I927, I had the opportunity to meet him in Brussels at the Fifth Physical Conference of the Solvay Institute, which was devoted to the theme 'Electrons and Photons.' At the Solvay meetings, Einstein had from their beginning been a most prominent figure, and several of us came to the conference with great anticipations to learn his reaction to the latest stage of the development which, to our view, went far in clarifying the problems which he had himself from the outset elicited so ingeniously. During the discussions, where the whole subject was reviewed by contributions from many sides and where also the arguments mentioned in the preceding pages were again presented, Einstein expressed, however, a deep concern over the extent to which causal account in space and time was abandoned in quantum mechanics.
To illustrate his attitude, Einstein referred at one of the sessions [9] to the simple example, illustrated by Fig. I, of a particle (electron or photon) penetrating through a hole or a narrow slit in a diaphragm placed at some distance before a photographic plate. On account of the diffraction of the wave
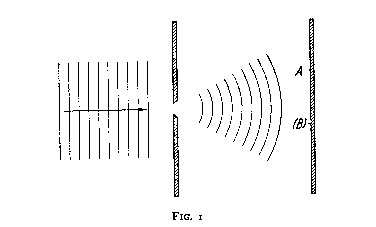
Fig. 1
connected with the motion of the particle and indicated in the figure by the thin lines, it is under such conditions not possible to predict with certainty at what point the electron will arrive at the photographic plate, but only to calculate the probability that, in an experiment, the electron will be found within any given region of the plate. The apparent difficulty, in this description, which Einstein felt so acutely, is the fact that, if in the experiment the electron is recorded at one point A of the plate, then it is out of the question of ever observing an effect of this electron at another point (B), although the laws of ordinary wave propagation offer no room for a correlation between two such events.
Einstein's attitude gave rise to ardent discussions within a small circle, in which Ehrenfest, who through the years had been a close friend of us both, took part in a most active and helpful way. Surely, we all recognized that, in the above example, the situation presents no analogue to the application of statistics in dealing with complicated mechanical systems, but rather recalled the background for Einstein's own early conclusions about the unidirection of individual radiation effects which contrasts so strongly with a simple wave picture (cf. p. 205). The discussions, however, centered on the question of whether the quantum-mechanical description exhausted the possibilities of accounting for observable phenomena or, as Einstein maintained, the analysis could be carried further and, especially, of whether a fuller description of the phenomena could be obtained by bringing into consideration the detailed balance of energy and momentum in individual processes.
To explain the trend of Einstein's arguments, it may be illustrative here to consider some simple features of the momentum and energy balance in connection with the location of a particle in space and time. For this purpose, we shall examine the simple case of a particle penetrating through a hole in a diaphragm without or with a shutter to open and close the hole, as indicated in Figs. 2a and 2b, respectively. The equidistant parallel lines to the left in the figures indicate the train of plane waves corresponding to the state of motion of a particle which, before reaching the diaphragm, has a momentum P related to the wave-number ![]() by the second of equations (I). In accordance with the diffraction of the waves when passing through the hole, the state of motion of the particle to the right of the diaphragm is represented by a spherical wave train with a suitably defined angular aperture
by the second of equations (I). In accordance with the diffraction of the waves when passing through the hole, the state of motion of the particle to the right of the diaphragm is represented by a spherical wave train with a suitably defined angular aperture ![]() and, in case of Fig. 2b, also with a limited radial extension. Consequently, the description of this state involves a certain latitude
and, in case of Fig. 2b, also with a limited radial extension. Consequently, the description of this state involves a certain latitude ![]() p in the momentum component of the particle parallel to the diaphragm and, in the case of a diaphragm with a shutter, an additional latitude
p in the momentum component of the particle parallel to the diaphragm and, in the case of a diaphragm with a shutter, an additional latitude ![]() E of the kinetic energy.
E of the kinetic energy.
Since a measure for the latitude ![]() q in location of the particle in the plane of the diaphragm is given by the radius a of the hole, and since
q in location of the particle in the plane of the diaphragm is given by the radius a of the hole, and since ![]()
![]() (I/
(I/ ![]() a), we get, using (I), just
a), we get, using (I), just ![]() p
p ![]()
![]() P
P ![]() (h/
(h/![]() q), in accordance with the indeterminacy relation (3). This result could, of course, also be obtained directly by noticing that, due to the limited extension of the wave-field at the place of the slit, the component of the wave-number parallel to the plane of the diaphragm will involve a latitude
q), in accordance with the indeterminacy relation (3). This result could, of course, also be obtained directly by noticing that, due to the limited extension of the wave-field at the place of the slit, the component of the wave-number parallel to the plane of the diaphragm will involve a latitude ![]()
![]()
![]() ( I/a)
( I/a) ![]() ( I /
( I /![]() q). Similarly, the spread of the frequencies
q). Similarly, the spread of the frequencies
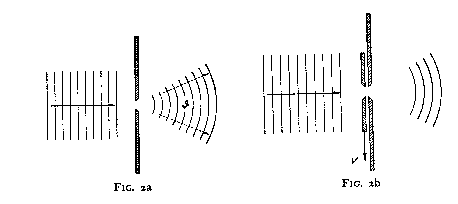
Fig. 2a, Fig 2b
of the harmonic components in the limited wave-train in Fig. 2b is evidently ![]()
![]()
![]() (I/
(I/![]() t), where
t), where ![]() t is the time interval during which the shutter leaves the hole open and, thus, represents the latitude in time of the passage of the particle through the diaphragm. From (I), we therefore get
t is the time interval during which the shutter leaves the hole open and, thus, represents the latitude in time of the passage of the particle through the diaphragm. From (I), we therefore get ![]() E
E ![]() t
t ![]() h, (4) again in accordance with the relation (3) for the two conjugated variables E and t.
h, (4) again in accordance with the relation (3) for the two conjugated variables E and t.
From the point of view of the laws of conservation, the origin of such latitudes entering into the description of the state of the particle after passing through the hole may be traced to the possibilities of momentum and energy exchange with the diaphragm or the shutter. In the reference system considered in Figs. 2a and 2b, the velocity of the diaphragm may be disregarded and only a change of momentum ![]() p between the particle and the diaphragm needs to be taken into consideration. The shutter, however, which leaves the hole opened during the time
p between the particle and the diaphragm needs to be taken into consideration. The shutter, however, which leaves the hole opened during the time ![]() t, moves with a considerable velocity v
t, moves with a considerable velocity v ![]() (a/
(a/![]() t), and a momentum transfer
t), and a momentum transfer ![]() p involves therefore an energy exchange with the particle, amounting to v
p involves therefore an energy exchange with the particle, amounting to v![]() p
p ![]() (I/
(I/![]() t)
t) ![]() q
q ![]() p
p ![]() (h/
(h/![]() t), being just of the same order of magnitude as the latitude
t), being just of the same order of magnitude as the latitude ![]() E given by (4) and, thus, allowing for momentum and energy balance.
E given by (4) and, thus, allowing for momentum and energy balance.
The problem raised by Einstein was now to what extent a control of the momentum and energy transfer, involved in a location of the particle in space and time, can be used for a further specification of the state of the particle after passing through the hole. Here, it must be taken into consideration that the position and the motion of the diaphragm and the shutter have so far been assumed to be accurately co-ordinated with the space-time reference frame. This assumption implies, in the description of the state of these bodies, an essential latitude as to their momentum and energy which need not, of course, noticeably affect the velocities, if the diaphragm and the shutter are sufficiently heavy. However, as soon as we want to know the momentum and energy of these parts of the measuring arrangement with an accuracy sufficient to control the momentum and energy exchange with the particle under investigation, we shall, in accordance with the general indeterminacy relations, lose the possibility of their accurate location in space and time. We have, therefore, to examine how far this circumstance will affect the intended use of the whole arrangement and, as we shall see, this crucial point clearly brings out the complementary character of the phenomena.
Returning for a moment to the case of the simple arrangement indicated in Fig. I, it has so far not been specified to what use it is intended. In fact, it is only on the assumption that the diaphragm and the plate have well-defined positions in space that it is impossible, within the frame of the quantum-mechanical formalism, to make more detailed predictions as to the point of the photographic plate where the particle will be recorded. If, however, we admit a sufficiently large latitude in the knowledge of the position of the diaphragm it should, in principle, be possible to control the momentum transfer to the diaphragm and, thus, to make more detailed predictions as to the direction of the electron path from the hole to the recording port. As regards the quantum-mechanical description, we have to deal here with a two-body system consisting of the diaphragm as well as of the particle, and it is just with an explicit application of conservation laws to such a system that we are concerned in the Compton effect where, for instance, the observation of the recoil of the electron by means of a cloud chamber allows us to predict in what direction the scattered photon will eventually be observed.
The importance of considerations of this kind was, in the course of the discussions, most interestingly illuminated by the examination of an arrangement where between the diaphragm with the slit and the photographic plate is inserted another
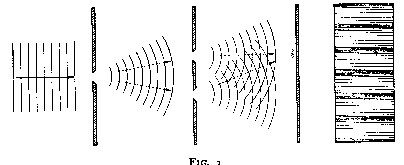
Fig. 3
diaphragm with two parallel slits, as is shown in Fig. 3. If a parallel beam of electrons (or photons) falls from the left on the first diaphragm, we shall, under usual conditions, observe on the plate an interference pattern indicated by the shading of the photographic plate shown in front view to the right of the figure. With intense beams, this pattern is built up by the accumulation of a large number of individual processes, each giving rise to a small spot on the photographic plate, and the distribution of these spots follows a simple law derivable from the wave analysis. The same distribution should also be found in the statistical account of many experiments performed with beams so faint that in a single exposure only one electron (or photon) will arrive at the photographic plate at some spot shown in the figure as a small star. Since, now, as indicated by the broken arrows, the momentum transferred to the first diaphragm ought to be different if the electron was assumed to pass through the upper or the lower slit in the second diaphragm, Einstein suggested that a control of the momentum transfer would permit a closer analysis of the phenomenon and, in particular, to decide through which of the two slits the electron had passed before arriving at the plate.
A closer examination showed, however, that the suggested control of the momentum transfer would involve a latitude in the knowledge of the position of the diaphragm which would exclude the appearance of the interference phenomena in question. In fact, if ![]() is the small angle between the conjectured paths of a particle passing through the upper or the lower slit, the difference of momentum transfer in these two cases will, according to (I), be equal to h
is the small angle between the conjectured paths of a particle passing through the upper or the lower slit, the difference of momentum transfer in these two cases will, according to (I), be equal to h ![]()
![]() and any control of the momentum of the diaphragm with an accuracy sufficient to measure this difference will, due to the indeterminacy relation, involve a minimum latitude of the position of the diaphragm, comparable with I/
and any control of the momentum of the diaphragm with an accuracy sufficient to measure this difference will, due to the indeterminacy relation, involve a minimum latitude of the position of the diaphragm, comparable with I/![]()
![]() . If, as in the figure, the diaphragm with the two slits is placed in the middle between the first diaphragm and the photographic plate, it will be seen that the number of fringes per unit length will be just equal to
. If, as in the figure, the diaphragm with the two slits is placed in the middle between the first diaphragm and the photographic plate, it will be seen that the number of fringes per unit length will be just equal to ![]()
![]() and, since an uncertainty in the position of the first diaphragm of the amount of I/
and, since an uncertainty in the position of the first diaphragm of the amount of I/![]()
![]() will cause an equal uncertainty in the positions of the fringes, it follows that no interference effect can appear. The same result is easily shown to hold for any other placing of the second diaphragm between the first diaphragm and the plate, and would also be obtained if, instead of the first diaphragm, another of these three bodies were used for the control, for the purpose suggested, of the momentum transfer.
will cause an equal uncertainty in the positions of the fringes, it follows that no interference effect can appear. The same result is easily shown to hold for any other placing of the second diaphragm between the first diaphragm and the plate, and would also be obtained if, instead of the first diaphragm, another of these three bodies were used for the control, for the purpose suggested, of the momentum transfer.
This point is of great logical consequence, since it is only the circumstance that we are presented with a choice of either tracing the path of a particle or observing interference effects, which allows us to escape from the paradoxical necessity of concluding that the behaviour of an electron or a photon should depend on the presence of a slit in the diaphragm through which it could be proved not to pass. We have here to do with a typical example of how the complementary phenomena appear under mutually exclusive experimental arrangements (cf. p. 2IO) and are just faced with the impossibility, in the analysis of quantum effects, of drawing any sharp separation between an independent behaviour of atomic objects and their interaction with the measuring instruments which serve to define the conditions under which the phenomena occur.
Our talks about the attitude to be taken in face of a novel situation as regards analysis and synthesis of experience touched naturally on many aspects of philosophical thinking, but, in spite of all divergencies of approach and opinion, a most humorous spirit animated the discussions. On his side, Einstein mockingly asked us whether we could really believe that the providential authorities took recourse to dice-playing ('. . . ob der liebe Gott wurfelt'), to which I replied by pointing at the great caution, already called for by ancient thinkers, in ascribing attributes to Providence in every-day language. I remember also how at the peak of the discussion Ehrenfest, in his affectionate manner of teasing his friends, jokingly hinted at the apparent similarity between Einstein's attitude and that of the opponents of relativity theory; but instantly Ehrenfest added that he would not be able to find relief in his own mind before concord with Einstein was reached.
Einstein's concern and criticism provided a most valuable incentive for us all to reexamine the various aspects of the situation as regards the description of atomic phenomena. To me it was a welcome stimulus to clarify still further the role played by the measuring instruments and, in order to bring into strong relief the mutually exclusive character of the experimental conditions under which the complementary phenomena appear, I tried in those days to sketch various apparatus in a pseudo-realistic style of which the following figures are examples. Thus, for the study of an interference phenomenon of the type indicated in Fig. 3, it suggests itself to use an experimental arrangement like that shown in Fig. 4, where the solid parts of the apparatus, serving as diaphragms and plate-holder, are
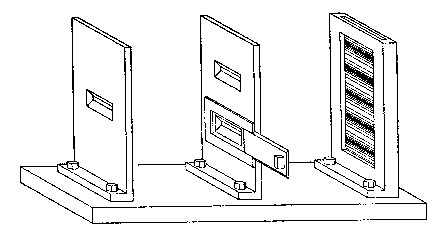
Fig. 4
firmly bolted to a common support. In such an arrangement, where the knowledge of the relative positions of the diaphragms and the photographic plate is secured by a rigid connection, it is obviously impossible to control the momentum exchanged between the particle and the separate parts of the apparatus. The only way in which, in such an arrangement, we could insure that the particle passed through one of the slits in the second diaphragm is to cover the other slit by a lid, as indicated in the figure; but if the slit is covered, there is of course no question of any interference phenomenon, and on the plate we shall simply observe a continuous distribution as in the case of the single fixed diaphragm in Fig. I.
In the study of phenomena in the account of which we are dealing with detailed momentum balance, certain parts of the whole device must naturally be given the freedom to move independently of others. Such an apparatus is sketched in Fig. 5, where a diaphragm with a slit is suspended by weak springs from a solid yoke bolted to the support on which also other immobile parts of the arrangement are to be fastened. The scale on the diaphragm together with the pointer on the bearings of the yoke refer to such study of the motion of the diaphragm, as may be required for an estimate of the momentum transferred to it, permitting one to draw conclusions as to the deflection suffered by the particle in passing through the slit. Since, however, any reading of the scale, in whatever way performed, will
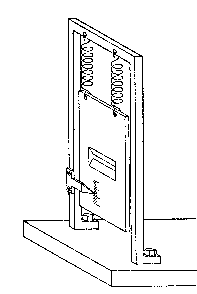
Fig. 5
involve an uncontrollable change in the momentum of the diaphragm, there will always be, in conformity with the indeterminacy principle, a reciprocal relationship between our knowledge of the position of the slit and the accuracy of the momentum control.
In the same semi-serious style, Fig. 6 represents a part of an arrangement suited for the study of phenomena which, in contrast to those just discussed, involve time co-ordination explicitly. It consists of a shutter rigidly connected with a robust clock resting on the support which carries a diaphragm and on which further parts of similar character, regulated by the same clock-work or by other clocks standardized relatively to it, are also to be fixed. The special aim of the figure is to underline that a clock is a piece of machinery, the working of which can completely be accounted for by ordinary mechanics and will be affected neither by reading of the position of its hands nor by the interaction between its accessories and an atomic particle. In securing the opening of the hole at a definite moment, an apparatus of this type might, for instance, be used for an accurate measurement of the time an electron or a photon takes to come from the diaphragm to some other place, but evidently, it would leave no possibility of controlling the energy transfer to
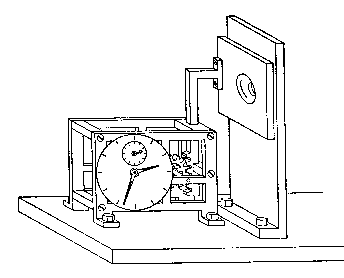
Fig. 6
the shutter with the aim of drawing conclusions as to the energy of the particle which has passed through the diaphragm. If we are interested in such conclusions we must, of course, use an arrangement where the shutter devices can no longer serve as accurate clocks, but where the knowledge of the moment when the hole in the diaphragm is open involves a latitude connected with the accuracy of the energy measurement by the general relation (4).
The contemplation of such more or less practical arrangements and their more or less fictitious use proved most instructive in directing attention to essential features of the problems. The main point here is the distinction between the objects under investigation and the measuring instruments which serve to define, in classical terms, the conditions under which the phenomena appear. Incidentally, we may remark that, for the illustration of the preceding considerations, it is not relevant that experiments involving an accurate control of the momentum or energy transfer from atomic particles to heavy bodies like diaphragms and shutters would be very difficult to perform, if practicable at all. It is only decisive that, in contrast to the proper measuring instruments, these bodies together with the particles would in such a case constitute the system to which the quantum-mechanical formalism has to be applied. As regards the specification of the conditions for any well-defined application of the formalism, it is moreover essential that the whole experimental arrangement be taken into account. In fact, the introduction of any further piece of apparatus, like a mirror, in the way of a particle might imply new interference effects essentially influencing the predictions as regards the results to be eventually recorded.
The extent to which renunciation of the visualization of atomic phenomena is imposed upon us by the impossibility of their subdivision is strikingly illustrated by the following example to which Einstein very early called attention and often has reverted. If a semi-reflecting mirror is placed in the way of a photon, leaving two possibilities for its direction of propagation, the photon may either be recorded on one, and only one, of two photographic plates situated at great distances in the two directions in question, or else we may, by replacing the plates by mirrors, observe effects exhibiting an interference between the two reflected wave-trains. In any attempt of a pictorial representation of the behaviour of the photon we would, thus, meet with the difficulty: to be obliged to say, on the one hand, that the photon always chooses one of the two ways and, on the other hand, that it behaves as if it had passed both ways.
It is just arguments of this kind which recall the impossibility of subdividing quantum phenomena and reveal the ambiguity in ascribing customary physical attributes to atomic objects. In particular, it must be realized that--besides in the account of the placing and timing of the instruments forming the experimental arrangement--all unambiguous use of space-time concepts in the description of atomic phenomena is confined to the recording of observations which refer to marks on a photographic plate or to similar practically irreversible amplification effects like the building of a water drop around an ion in a cloud-chamber. Although, of course, the existence of the quantum of action is ultimately responsible for the properties of the materials of which the measuring instruments are built and on which the functioning of the recording devices depends, this circumstance is not relevant for the problems of the adequacy and completeness of the quantum-mechanical description in its aspects here discussed.
These problems were instructively commented upon from different sides at the Solvay meeting [10], in the same session where Einstein raised his general objections. On that occasion an interesting discussion arose also about how to speak of the appearance of phenomena for which only predictions of statistical character can be made. The question was whether, as to the occurrence of individual effects, we should adopt a terminology proposed by Dirac, that we were concerned with a choice on the part of 'nature' or, as suggested by Heisenberg, we should say that we have to do with a choice on the part of the 'observer' constructing the measuring instruments and reading their recording. Any such terminology would, however, appear dubious since, on the one hand, it is hardly reasonable to endow nature with volition in the ordinary sense, while, on the other hand, it is certainly not possible for the observer to influence the events which may appear under the conditions he has arranged. To my mind, there is no other alternative than to admit that, in this field of experience, we are dealing with individual phenomena and that our possibilities of handling the measuring instruments allow us only to make a choice between the different complementary types of phenomena we want to study.
The epistemological problems touched upon here were more explicitly dealt with in my contribution to the issue of Naturwissenschaften in celebration of Planck's 70th birthday in I929. In this article, a comparison was also made between the lesson derived from the discovery of the universal quantum of action and the development which has followed the discovery of the finite velocity of light and which, through Einstein's pioneer work, has so greatly clarified basic principles of natural philosophy. In relativity theory, the emphasis on the dependence of all phenomena on the reference frame opened quite new ways of tracing general physical laws of unparalleled scope. In quantum theory, it was argued, the logical comprehension of hitherto unsuspected fundamental regularities governing atomic phenomena has demanded the recognition that no sharp separation can be made between an independent behaviour of the objects and their interaction with the measuring instruments which define the reference frame.
In this respect, quantum theory presents us with a novel situation in physical science, but attention was called to the very close analogy with the situation as regards analysis and synthesis of experience, which we meet in many other fields of human knowledge and interest. As is well known, many of the difficulties in psychology originate in the different placing of the separation lines between object and subject in the analysis of various aspects of psychical experience. Actually, words like 'thoughts' and 'sentiments,' equally indispensable to illustrate the variety and scope of conscious life, are used in a similar complementary way as are space-time co-ordination and dynamical conservation laws in atomic physics. A precise formulation of such analogies involves, of course, intricacies of terminology, and the writer's position is perhaps best indicated in a passage in the article, hinting at the mutually exclusive relationship which will always exist between the practical use of any word and attempts at its strict definition. The principal aim, however, of these considerations, which were not least inspired by the hope of influencing Einstein's attitude, was to point to perspectives of bringing general epistemological problems into relief by means of a lesson derived from the study of new, but fundamentally simple physical experience.
At the next meeting with Einstein at the Solvay Conference in I930, our discussions took quite a dramatic turn. As an objection to the view that a control of the interchange of momentum and energy between the objects and the measuring instruments was excluded if these instruments should serve their purpose of defining the space-time frame of the phenomena, Einstein brought forward the argument that such control should be possible when the exigencies of relativity theory were taken into consideration. In particular, the general relationship between energy and mass, expressed in Einstein's famous formula E = mc2 (5) should allow, by means of simple weighing, to measure the total energy of any system and, thus, in principle to control the energy transferred to it when it interacts with an atomic object.
As an arrangement suited for such purpose, Einstein proposed the device indicated in Fig. 7, consisting of a box with
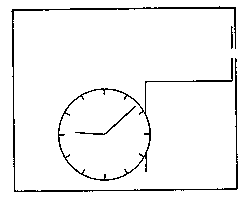
Fig. 7
a hole in its side, which could be opened or closed by a shutter moved by means of a clock-work within the box. If, in the beginning, the box contained a certain amount of radiation and the clock was set to open the shutter for a very short interval at a chosen time, it could be achieved that a single photon was released through the hole at a moment known with as great accuracy as desired. Moreover, it would apparently also be possible, by weighing the whole box before and after this event, to measure the energy of the photon with any accuracy wanted, in definite contradiction to the reciprocal indeterminacy of time and energy quantities in quantum mechanics.
This argument amounted to a serious challenge and gave rise to a thorough examination of the whole problem. At the outcome of the discussion, to which Einstein himself contributed effectively, it became clear, however, that this argument could not be upheld. In fact, in the consideration of the problem, it was found necessary to look closer into the consequences of the identification of inertial and gravitational mass implied in the application of relation (5). Especially, it was essential to take into account the relationship between the rate of a clock and its position in a gravitational field--well known from the red-shift of the lines in the sun's spectrum--following from Einstein's principle of equivalence between gravity effects and the phenomena observed in accelerated reference frames.
Our discussion concentrated on the possible application of an apparatus incorporating Einstein's device and drawn in Fig. 8 in the same pseudo-realistic style as some of the preceding figures. The box, of which a section is shown in order to exhibit its interior, is suspended in a spring-balance and is furnished with a pointer to read its position on a scale fixed to the balance support. The weighing of the box may thus be performed with any given accuracy ![]() m by adjusting the balance to its zero position by means of suitable loads. The essential point is now that any determination of this position with a given accuracy
m by adjusting the balance to its zero position by means of suitable loads. The essential point is now that any determination of this position with a given accuracy ![]() q will involve a minimum latitude
q will involve a minimum latitude ![]() p in the control of the momentum of the box connected with
p in the control of the momentum of the box connected with ![]() q by the relation (3). This latitude must obviously again be smaller than the total impulse which, during the whole interval T of the balancing procedure, can be given by the gravitational field to a body with a mass
q by the relation (3). This latitude must obviously again be smaller than the total impulse which, during the whole interval T of the balancing procedure, can be given by the gravitational field to a body with a mass ![]() m, or
m, or
![]() p
p ![]()
![]() T g
T g ![]() m (6)
m (6)
where g is the gravity constant. The greater the accuracy of the reading q of the pointer, the longer must, consequently, be the balancing interval T, if a given accuracy ![]() m of the weighing of the box with its content shall be obtained.
m of the weighing of the box with its content shall be obtained.
Now, according to general relativity theory, a clock, when displaced in the direction of the gravitational force by an amount of ![]() q, will change its rate in such a way that its reading
q, will change its rate in such a way that its reading
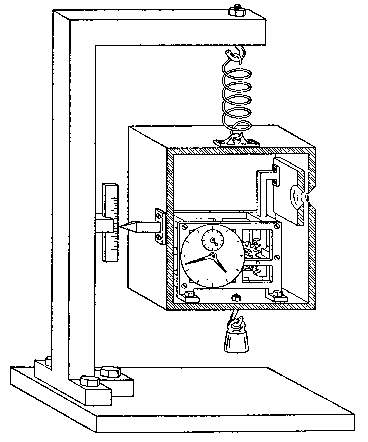
Fig. 8
in the course of a time interval T will differ by an amount ![]() T given by the relation
T given by the relation ![]() =
= ![]() g
g ![]() q (7) By comparing (6) and (7) we see, therefore, that after the weighing procedure there will in our knowledge of the adjustment of the clock be a latitude
q (7) By comparing (6) and (7) we see, therefore, that after the weighing procedure there will in our knowledge of the adjustment of the clock be a latitude ![]() T >
T > ![]() . Together with the formula (5), this relation again leads to
. Together with the formula (5), this relation again leads to ![]() T
T ![]() E > h, in accordance with the indeterminacy principle. Consequently, a use of the apparatus as a means of accurately measuring the energy of the photon will prevent us from controlling the moment of its escape.
E > h, in accordance with the indeterminacy principle. Consequently, a use of the apparatus as a means of accurately measuring the energy of the photon will prevent us from controlling the moment of its escape.
The discussion, so illustrative of the power and consistency of relativistic arguments, thus emphasized once more the necessity of distinguishing, in the study of atomic phenomena, between the proper measuring instruments which serve to define the reference frame and those parts which are to be regarded as objects under investigation and in the account of which quantum effects cannot be disregarded. Notwithstanding the most suggestive confirmation of the soundness and wide scope of the quantum-mechanical way of description, Einstein nevertheless, in a following conversation with me, expressed a feeling of disquietude as regards the apparent lack of firmly laid down principles for the explanation of nature, in which all could agree. From my viewpoint, however, I could only answer that, in dealing with the task of bringing order into an entirely new field of experience, we could hardly trust in any accustomed principles, however broad, apart from the demand of avoiding logical inconsistencies and, in this respect, the mathematical formalism of quantum mechanics should surely meet all requirements.
The Solvay meeting in 1930 was the last occasion where, in common discussions with Einstein, we could benefit from the stimulating and mediating influence of Ehrenfest, but shortly before his deeply deplored death in I933 he told me that Einstein was far from satisfied and with his usual acuteness had discerned new aspects of the situation which strengthened his critical attitude. In fact, by further examining the possibilities for the application of a balance arrangement, Einstein had perceived alternative procedures which, even if they did not allow the use he originally intended, might seem to enhance the paradoxes beyond the possibilities of logical solution. Thus, Einstein had pointed out that, after a preliminary weighing of the box with the clock and the subsequent escape of the photon, one was still left with the choice of either repeating the weighing or opening the box and comparing the reading of the clock with the standard time scale. Consequently, we are at this stage still free to choose whether we want to draw conclusions either about the energy of the photon or about the moment when it left the box. Without in any way interfering with the photon between its escape and its later interaction with other suitable measuring instruments, we are, thus, able to make accurate predictions pertaining either to the moment of its arrival or to the amount of energy liberated by its absorption. Since, however, according to the quantum-mechanical formalism, the specification of the state of an isolated particle cannot involve both a well-defined connection with the time scale and an accurate fixation of the energy, it might thus appear as if this formalism did not offer the means of an adequate description.
Once more Einstein's searching spirit had elicited a peculiar aspect of the situation in quantum theory, which in a most striking manner illustrated how far we have here transcended customary explanation of natural phenomena. Still, I could not agree with the trend of his remarks as reported by Ehrenfest. In my opinion, there could be no other way to deem a logically consistent mathematical formalism as inadequate than by demonstrating the departure of its consequences from experience or by proving that its predictions did not exhaust the possibilities of observation, and Einstein's argumentation could be directed to neither of these ends. In fact, we must realize that in the problem in question we are not dealing with a single specified experimental arrangement, but are referring to two different, mutually exclusive arrangements. In the one, the balance together with another piece of apparatus like a spectrometer is used for the study of the energy transfer by a photon; in the other, a shutter regulated by a standardized clock together with another apparatus of similar kind, accurately timed relatively to the clock, is used for the study of the time of propagation of a photon over a given distance. In both these cases, as also assumed by Einstein, the observable effects are expected to be in complete conformity with the predictions of the theory.
The problem again emphasizes the necessity of considering the whole experimental arrangement, the specification of which is imperative for any well-defined application of the quantum-mechanical formalism. Incidentally, it may be added that paradoxes of the kind contemplated by Einstein are encountered also in such simple arrangements as sketched in Fig. 5. In fact, after a preliminary measurement of the momentum of the diaphragm, we are in principle offered the choice, when an electron or photon has passed through the slit, either to repeat the momentum measurement or to control the position of the diaphragm and, thus, to make predictions pertaining to alternative subsequent observations. It may also be added that it obviously can make no difference as regards observable effects obtainable by a definite experimental arrangement, whether our plans of constructing or handling the instruments are fixed beforehand or whether we prefer to postpone the completion of our planning until a later moment when the particle is already on its way from one instrument to another.
In the quantum-mechanical description our freedom of constructing and handling the experimental arrangement finds its proper expression in the possibility of choosing the classically defined parameters entering in any proper application of the formalism. Indeed, in all such respects quantum mechanics exhibits a correspondence with the state of affairs familiar from classical physics, which is as close as possible when considering the individuality inherent in the quantum phenomena. Just in helping to bring out this point so clearly, Einstein's concern had therefore again been a most welcome incitement to explore the essential aspects of the situation.
The next Solvay meeting in I933 was devoted to the problems of the structure and properties of atomic nuclei, in which field such great advances were made just in that period due to the experimental discoveries as well as to new fruitful applications of quantum mechanics. It need in this connection hardly be recalled that just the evidence obtained by the study of artificial nuclear transformations gave a most direct test of Einstein's fundamental law regarding the equivalence of mass and energy, which was to prove an evermore important guide for researches in nuclear physics. It may also be mentioned how Einstein's intuitive recognition of the intimate relationship between the law of radioactive transformations and the probability rules governing individual radiation effects (cf. p. 205) was confirmed by the quantum-mechanical explanation of spontaneous nuclear disintegrations. In fact, we are here dealing with a typical example of the statistical mode of description, and the complementary relationship between energy-momentum conservation and time-space co-ordination is most strikingly exhibited in the well-known paradox of particle penetration through potential barriers.
Einstein himself did not attend this meeting, which took place at a time darkened by the tragic developments in the political world which were to influence his fate so deeply and add so greatly to his burdens in the service of humanity. A few months earlier, on a visit to Princeton where Einstein was then guest of the newly founded Institute for Advanced Study to which he soon after became permanently attached, I had, however, opportunity to talk with him again about the epistemological aspects of atomic physics, but the difference between our ways of approach and expression still presented obstacles to mutual understanding. While, so far, relatively few persons had taken part in the discussions reported in this article, Einstein's critical attitude towards the views on quantum theory adhered to by many physicists was soon after brought to public attention through a paper [11] with the title 'Can Quantum-Mechanical Description of Physical Reality Be Considered Complete?,' published in I935 by Einstein, Podolsky and Rosen.
The argumentation in this paper is based on a criterion which the authors express in the following sentence: 'If, without in any way disturbing a system, we can predict with certainty (i.e., with probability equal to unity) the value of a physical quantity, then there exists an element of physical reality corresponding to this physical quantity.' By an elegant exposition of the consequences of the quantum-mechanical formalism as regards the representation of a state of a system, consisting of two parts which have been in interaction for a limited time interval, it is next shown that different quantities, the fixation of which cannot be combined in the representation of one of the partial systems, can nevertheless be predicted by measurements pertaining to the other partial system. According to their criterion, the authors therefore conclude that quantum mechanics does not 'provide a complete description of the physical reality,' and they express their belief that it should be possible to develop a more adequate account of the phenomena.
Due to the lucidity and apparently incontestable character of the argument, the paper of Einstein, Podolsky and Rosen created a stir among physicists and has played a large role in general philosophical discussion. Certainly the issue is of a very subtle character and suited to emphasize how far, in quantum theory, we are beyond the reach of pictorial visualization. It will be seen, however, that we are here dealing with problems of just the same kind as those raised by Einstein in previous discussions, and, in an article which appeared a few months later [12], I tried to show that from the point of view of complementarity the apparent inconsistencies were completely removed. The trend of the argumentation was in substance the same as that exposed in the foregoing pages, but the aim of recalling the way in which the situation was discussed at that time may be an apology for citing certain passages from my article.
Thus, after referring to the conclusions derived by Einstein, Podolsky and Rosen on the basis of their criterion, I wrote:
Such an argumentation, however, would hardly seem suited to affect the soundness of quantum-mechanical description, which is based on a coherent mathematical formalism covering automatically any procedure of measurement like that indicated. The apparent contradiction in fact discloses only an essential inadequacy of the customary viewpoint of natural philosophy for a rational account of physical phenomena of the type with which we are concerned in quantum mechanics. Indeed the finite interaction between object and measuring agencies conditioned by the very existence of the quantum of action entails - because of the impossibility of controlling the reaction of the object on the measuring instruments, if these are to serve their purpose - the necessity of a final renunciation of the classical ideal of causality and a radical revision of our attitude towards the problem of physical reality. In fact, as we shall see, a criterion of reality like that proposed by the named authors contains - however cautious its formulation may appear - an essential ambiguity when it is applied to the actual problems with which we are here concerned.
As regards the special problem treated by Einstein, Podolsky and Rosen, it was next shown that the consequences of the formalism as regards the representation of the state of a system consisting of two interacting atomic objects correspond to the simple arguments mentioned in the preceding in connection with the discussion of the experimental arrangements suited for the study of complementary phenomena. In fact, although any pair q and p, of conjugate space and momentum variables obeys the rule of non-commutative multiplication expressed by (2), and can thus only be fixed with reciprocal latitudes given by (3), the difference q1- q2 between two space-co-ordinates referring to the constituents of the system will commute with the sum pl + p2 of the corresponding momentum components, as follows directly from the commutability of ql with p2 and q2 with pl. Both ql--q2 and pl + p2 can, therefore, be accurately fixed in a state of the complex system and, consequently, we can predict the values of either q1 or pl if either q2 or p2, respectively, are determined by direct measurements. If, for the two parts of the system, we take a particle and a diaphragm, like that sketched in Fig. 5, we see that the possibilities of specifying the state of the particle by measurements on the diaphragm just correspond to the situation described on p. 220 and further discussed on p. 230, where it was mentioned that, after the particle has passed through the diaphragm, we have in principle the choice of measuring either the position of the diaphragm or its momentum and, in each case, to make predictions as to subsequent observations pertaining to the particle. As repeatedly stressed, the principal point is here that such measurements demand mutually exclusive experimental arrangements.
The argumentation of the article was summarized in the following passage:
From our point of view we now see that the wording of the abovementioned criterion of physical reality proposed by Einstein, Podolsky, and Rosen contains an ambiguity as regards the meaning of the expression without in any way disturbing a system.' Of course there is in a case like that just considered no question of a mechanical disturbance of the system under investigation during the last critical stage of the measuring procedure. But even at this stage there is essentially the question of an influence on the very conditions which define the possible types of predictions regarding the future behaviour of the system. Since these conditions constitute an inherent element of the description of any phenomenon to which the term 'physical reality' can be properly attached, we see that the argumentation of the mentioned authors does not justify their conclusion that quantum-mechanical description is essentially incomplete. On the contrary, this description, as appears from the preceding discussion, may be characterized as a rational utilization of all possibilities of unambiguous interpretation of measurements, compatible with the finite and uncontrollable interaction between the objects and the measuring instruments in the field of quantum theory. In fact, it is only the mutual exclusion of any two experimental procedures, permitting the unambiguous definition of complementary physical quantities, which provides room for new physical laws, the coexistence of which might at first sight appear irreconcilable with the basic principles of science. It is just this entirely new situation as regards the description of physical phenomena that the notion of complementarity aims at characterizing.
Rereading these passages, I am deeply aware of the inefficiency of expression which must have made it very difficult to appreciate the trend of the argumentation aiming to bring out the essential ambiguity involved in a reference to physical attributes of objects when dealing with phenomena where no sharp distinction can be made between the behaviour of the objects themselves and their interaction with the measuring instruments. I hope, however, that the present account of the discussions with Einstein in the foregoing years, which contributed so greatly to make us familiar with the situation in quantum physics, may give a clearer impression of the necessity of a radical revision of basic principles for physical explanation in order to restore logical order in this field of experience.
Einstein's own views at that time are presented in an article 'Physics and Reality,' published in I936 in the Journal of the Franklin Institute [13]. Starting from a most illuminating exposition of the gradual development of the fundamental principles in the theories of classical physics and their relation to the problem of physical reality, Einstein here argues that the quantum-mechanical description is to be considered merely as a means of accounting for the average behaviour of a large number of atomic systems and his attitude to the belief that it should offer an exhaustive description of the individual phenomena is expressed in the following words: 'To believe this is logically possible without contradiction; but it is so very contrary to my scientific instinct that I cannot forego the search for a more complete conception.'
Even if such an attitude might seem well-balanced in itself, it nevertheless implies a rejection of the whole argumentation exposed in the preceding, aiming to show that, in quantum mechanics, we are not dealing with an arbitrary renunciation of a more detailed analysis of atomic phenomena, but with a recognition that such an analysis is in principle excluded. The peculiar individuality of the quantum effects presents us, as regards the comprehension of well-defined evidence, with a novel situation unforeseen in classical physics and irreconcilable with conventional ideas suited for our orientation and adjustment to ordinary experience. It is in this respect that quantum theory has called for a renewed revision of the foundation for the unambiguous use of elementary concepts, as a further step in the development which, since the advent of relativity theory, has been so characteristic of modern science.
In the following years, the more philosophical aspects of the situation in atomic physics aroused the interest of ever larger circles and were, in particular, discussed at the Second International Congress for the Unity of Science in Copenhagen in July I936. In a lecture on this occasion [14], I tried especially to stress the analogy in epistemological respects between the limitation imposed on the causal description in atomic physics and situations met with in other fields of knowledge. A principal purpose of such parallels was to call attention to the necessity in many domains of general human interest to face problems of a similar kind as those which had arisen in quantum theory and thereby to give a more familiar background for the apparently extravagant way of expression which physicists have developed to cope with their acute difficulties.
Besides the complementary features conspicuous in psychology and already touched upon (cf. p. 224), examples of such relationships can also be traced in biology, especially as regards the comparison between mechanistic and vitalistic viewpoints. Just with respect to the observational problem, this last question had previously been the subject of an address to the International Congress on Light Therapy held in Copenhagen in I932 [15], where it was incidentally pointed out that even the psycho-physical parallelism as envisaged by Leibniz and Spinoza has obtained a wider scope through the development of atomic physics, which forces us to an attitude towards the problem of explanation recalling ancient wisdom, that when searching for harmony in life one must never forget that in the drama of existence we are ourselves both actors and spectators.
Utterances of this kind would naturally in many minds evoke the' impression of an underlying mysticism foreign to the spirit of science; at the above mentioned Congress in I936 I therefore tried to clear up such misunderstandings and to explain that the only question was an endeavour to clarify the conditions, in each field of knowledge, for the analysis and synthesis of experience [14]. Yet, I am afraid that I had in this respect only little success in convincing my listeners, for whom the dissent among the physicists themselves was naturally a cause of scepticism as to the necessity of going so far in renouncing customary demands as regards the explanation of natural phenomena. Not least through a new discussion with Einstein in Princeton in I937, where we did not get beyond a humourous contest concerning which side Spinoza would have taken if he had lived to see the development of our days, I was strongly reminded of the importance of utmost caution in all questions of terminology and dialectics.
These aspects of the situation were especially discussed at a meeting in Warsaw in I938, arranged by the International Institute of Intellectual Co-operation of the League of Nations [16]. The preceding years had seen great progress in quantum physics due to a number of fundamental discoveries regarding the constitution and properties of atomic nuclei as well as due to important developments of the mathematical formalism taking the requirements of relativity theory into account. In the last respect, Dirac's ingenious quantum theory of the electron offered a most striking illustration of the power and fertility of the general quantum-mechanical way of description. In the phenomena of creation and annihilation of electron pairs we have in fact to do with new fundamental features of atomicity, which are intimately connected with the non-classical aspects of quantum statistics expressed in the exclusion principle, and which have demanded a still more far-reaching renunciation of explanation in terms of a pictorial representation.
Meanwhile, the discussion of the epistemological problems in atomic physics attracted as much attention as ever and, in commenting on Einstein's views as regards the incompleteness of the quantum-mechanical mode of description, I entered more directly on questions of terminology. In this connection I warned especially against phrases, often found in the physical literature, such as 'disturbing of phenomena by observation' or 'creating physical attributes to atomic objects by measurements.' Such phrases, which may serve to remind of the apparent paradoxes in quantum theory, are at the same time apt to cause confusion, since words like 'phenomena' and 'observations,' just as 'attributes' and 'measurements,' are used in a way hardly compatible with common language and practical definition.
As a more appropriate way of expression I advocated the application of the word phenomenon exclusively to refer to the observations obtained under specified circumstances, including an account of the whole experimental arrangement. In such terminology, the observational problem is free of any special intricacy since, in actual experiments, all observations are expressed by unambiguous statements referring, for instance, to the registration of the point at which an electron arrives at a photographic plate. Moreover, speaking in such a way is just suited to emphasize that the appropriate physical interpretation of the symbolic quantum-mechanical formalism amounts only to predictions, of determinate or statistical character, pertaining to individual phenomena appearing under conditions defined by classical physical concepts.
Notwithstanding all differences between the physical problems which have given rise to the development of relativity theory and quantum theory, respectively, a comparison of purely logical aspects of relativistic and complementary argumentation reveals striking similarities as regards the renunciation of the absolute significance of conventional physical attributes of objects. Also, the neglect of the atomic constitution of the measuring instruments themselves, in the account of actual experience, is equally characteristic of the applications of relativity and quantum theory. Thus, the smallness of the quantum of action compared with the actions involved in usual experience, including the arranging and handling of physical apparatus, is as essential in atomic physics as is the enormous number of atoms composing the world in the general theory of relativity which, as often pointed out, demands that dimensions of apparatus for measuring angles can be made small compared with the radius of curvature of space.
In the Warsaw lecture, I commented upon the use of not directly visualizable symbolism in relativity and quantum theory in the following way:
Even the formalisms, which in both theories within their scope offer adequate means of comprehending all conceivable experience, exhibit deepgoing analogies. In fact, the astounding simplicity of the generalization of classical physical theories, which are obtained by the use of multidimensional geometry and non-commutative algebra, respectively, rests in both cases essentially on the introduction of the conventional symbol ![]() . The abstract character of the formalisms concerned is indeed, on closer examination, as typical of relativity theory as it is of quantum mechanics, and it is in this respect purely a matter of tradition if the former theory is considered as a completion of classical physics rather than as a first fundamental step in the thoroughgoing revision of our conceptual means of comparing observations, which the modern development of physics has forced upon us.
. The abstract character of the formalisms concerned is indeed, on closer examination, as typical of relativity theory as it is of quantum mechanics, and it is in this respect purely a matter of tradition if the former theory is considered as a completion of classical physics rather than as a first fundamental step in the thoroughgoing revision of our conceptual means of comparing observations, which the modern development of physics has forced upon us.
It is, of course, true that in atomic physics we are confronted with a number of unsolved fundamental problems, especially as regards the intimate relationship between the elementary unit of electric charge and the universal quantum of action; but these problems are no more connected with the epistemological points here discussed than is the adequacy of relativistic argumentation with the issue of thus far unsolved problems of cosmology. Both in relativity and in quantum theory we are concerned with new aspects of scientific analysis and synthesis and, in this connection, it is interesting to note that, even in the great epoch of critical philosophy in the former century, there was only question to what extent a priori arguments could be given for the adequacy of space-time co-ordination and causal connection of experience, but never question of rational generalizations or inherent limitations of such categories of human thinking.
Although in more recent years I have had several occasions of meeting Einstein, the continued discussions, from which I always have received new impulses, have so far not led to a common view about the epistemological problems in atomic physics, and our opposing views are perhaps most clearly stated in a recent issue of Dialectica [17], bringing a general discussion of these problems. Realizing, however, the many obstacles for mutual understanding as regards a matter where approach and background must influence everyone's attitude, I have welcomed this opportunity of a broader exposition of the development by which, to my mind, a veritable crisis in physical science has been overcome. The lesson we have hereby received would seem to have brought us a decisive step further in the never-ending struggle for harmony between content and form, and taught us once again that no content can be grasped without a formal frame and that any form, however useful it has hitherto proved, may be found to be too narrow to comprehend new experience.
Surely, in a situation like this, where it has been difficult to reach mutual understanding not only between philosophers and physicists but even between physicists of different schools, the difficulties have their root not seldom in the preference for a certain use of language suggesting itself from the different lines of approach. In the Institute in Copenhagen, where through those years a number of young physicists from various countries came together for discussions, we used, when in trouble, often to comfort ourselves with jokes, among them the old saying of the two kinds of truth. To the one kind belong statements so simple and clear that the opposite assertion obvious]y could not be defended. The other kind, the so-called 'deep truths,' are statements in which the opposite also contains deep truth. Now, the development in a new field will usually pass through stages in which chaos becomes gradually replaced by order; but it is not least in the intermediate stage where deep truth prevails that the work is really exciting and inspires the imagination to search for a firmer hold. For such endeavours of seeking the proper balance between seriousness and humour, Einstein's own personality stands as a great example and, when expressing my belief that through a singularly fruitful co-operation of a whole generation of physicists we are nearing the goal where logical order to a large extent allows us to avoid deep truth, I hope that it will be taken in his spirit and may serve as an apology for several utterances in the preceding pages.
The discussions with Einstein which have formed the theme of this article have extended over many years which have witnessed great progress in the field of atomic physics. Whether our actual meetings have been of short or long duration, they have always left a deep and lasting impression on my mind, and when writing this report I have, so-to-say, been arguing with Einstein all the time even when entering on topics apparently far removed from the special problems under debate at our meetings. As regards the account of the conversations I am, of course, aware that I am relying only on my own memory, just as I am prepared for the possibility that many features of the development of quantum theory, in which Einstein has played so large a part, may appear to himself in a different light. I trust, however, that I have not failed in conveying a proper impression of how much it has meant to me to be able to benefit from the inspiration which we all derive from every contact with Einstein.
NIELS BOHR - UNIVERSITETETS INSTITUT FOR TEORETISK FYSIK COPENHAGEN, DENMARK
A. Einstein, Ann. d. Phys., I7, 132, (I905).
N. Bohr, Fysisk Tidsskrift, I2, 97, (1914), (The Theory of Spectra and Atomic Constitution, Cambridge, University Press, I922).
A. Einstein, Phys. Zs., 18, 121, (I9I7).
A. Einstein and P. Ehrenfest, Zs. f. Phys., II, 31 (I922).
N. Bohr, H. A. Kramers and J. C. Slater, Phil. Mag., 47, 785, (I924).
A. Einstein, Berl. Ber., (I924), 261, and (I925), 3 and 18.
W. Heisenberg, Zs. f. Phys., 43, I72, (I927). Atti del Congresso Internazionale dei Fisici, Como, Settembre 1927 (reprinted in Nature, I2I, 78 and 580, I928). Institut International de Physique Solvay, Rapport et discussions du 5e Conseil, Paris I 928, 253 ff. Ibid., 248ff.
A. Einstein, B. Podolsky and N. Rosen, Phys. Rev., 47, 777, (1935).
N. Bohr, Phys. Rev., 48, 696, (I935).
A. Einstein, Journ. Frankl. Inst., 22I, 349, (1936).
N. Bohr, Erkenntnis, 6, 293, (1937), and Philosophy of Science, 4, 289, (I937). Ile Congres international de la Lumiere, Copenhague 1932 (reprinted in Nature, I3I, 421 and 457, I933). New Theories in Physics (Paris 1938),
N. Bohr, Dialectica, I, 312 (1948).
Help Humanity
"You must be the change you wish to see in the world."
(Mohandas Gandhi)
 "When forced to summarize the general theory of relativity in one sentence:
Time and space and gravitation have no separate existence from matter. ... Physical objects are not in space, but these objects are spatially extended. In this way the concept 'empty space' loses its meaning. ... The particle can only appear as a limited region in space in which
the field strength or the energy density are particularly high. ...
"When forced to summarize the general theory of relativity in one sentence:
Time and space and gravitation have no separate existence from matter. ... Physical objects are not in space, but these objects are spatially extended. In this way the concept 'empty space' loses its meaning. ... The particle can only appear as a limited region in space in which
the field strength or the energy density are particularly high. ...
The free, unhampered exchange of ideas and scientific conclusions is necessary for the sound development of science, as it is in all spheres
of cultural life. ... We must not conceal from ourselves that no improvement in the present depressing situation is possible without
a severe struggle; for the handful of those who are really determined to do something is minute in comparison with the mass of the lukewarm
and the misguided. ...
Humanity is going to need a substantially new way of thinking if it is to survive!" (Albert Einstein)
 We can now deduce the most simple science theory of reality - the wave structure of matter in space. By understanding how we and everything around us are interconnected
in Space we can then deduce solutions to the fundamental problems of human knowledge in physics, philosophy, metaphysics, theology, education, health, evolution and ecology, politics and society.
We can now deduce the most simple science theory of reality - the wave structure of matter in space. By understanding how we and everything around us are interconnected
in Space we can then deduce solutions to the fundamental problems of human knowledge in physics, philosophy, metaphysics, theology, education, health, evolution and ecology, politics and society.
This is the profound new way of thinking that Einstein
realised, that we exist as spatially extended structures of the universe - the discrete and separate body an illusion. This simply confirms the
intuitions of the ancient philosophers and mystics.
Given the current censorship in physics / philosophy of science journals (based on the standard model of particle physics / big bang cosmology) the internet is the best hope for getting new knowledge
known to the world. But that depends on you, the people who care about science and society, realise the importance of truth and reality.
It is Easy to Help!
Just click on the Social Network links at top of page, or copy a nice image or quote you like and share it. We have a wonderful collection of knowledge from the greatest minds in human history, so people will appreciate your contributions. In doing this you will help a new generation of scientists see that there is a simple sensible explanation of physical reality (One Substance, One Law) - the source of truth and wisdom, the only cure for the madness of man! Thanks! Geoff Haselhurst (Updated May, 2025)
A new scientific truth does not triumph by convincing its opponents and making them see the light, but rather because its opponents eventually die, and a new generation grows up that is familiar with it. (Max Planck, 1920)
"All that is necessary for evil to succeed is for good people to do nothing."
(Edmund Burke)
"In a time of universal deceit - telling the truth is a revolutionary act."
(George Orwell)
"Hell is Truth Seen Too Late."
(Thomas Hobbes)
Legal Disclaimer and Privacy Policy












