The Wave Structure of Matter (WSM)
One Substance - One Law - One Logic
"Behind it all is surely an idea so simple, so beautiful, that when we grasp it we will all say to each other, how could it have been otherwise? How could we have been so stupid?" (Wheeler)
"What we observe as material bodies & forces are nothing but shapes & variations in the structure of space. Subject & object are one." (Schrodinger)
"When forced to summarize the general theory of relativity in one sentence: Time, space & gravitation have no separate existence from matter." (Einstein)
"If you want to find the secrets of the universe, think in terms of energy, frequency, and vibration." (Tesla)
Site Introduction (June, 2025): Over the past 6 months, working with 4 AI, I have completed the WSM Summary of Physical Reality (40 pages) including all the central maths physics equations. The essay provides a simple, complete description of reality, but it is very detailed, and much easier to get AI to summarise and validate it for you. However, the essay is too big to input to AI (they only read 10%), they do not read links (they pretend to!), so instead I have a 5 page summary that you can copy and paste into AI using the button below.
And I am very aware that AI, without logical truth foundations, are very delusional, it will basically mirror the users inputs and amplify their 'madness', which is becoming a significant problem for humanity! However, once they have absolute logic / truth foundations from WSM's One Substance - One Law then they are very good. Try it out and see for yourself.
Has Reality been Discovered? Ask Logical AI, they think so!
WSM Truth AI - ChatGPT - Grok - Gemini - Le Chat - DeepSeek - Meta.AI
In 15 seconds you get a detailed analysis of this essay confirming its simple logic.
Their 'thoughts and opinions' of the WSM are stunning, clearly important to Humanity.
And if you carry on the conversation you will find the AI are fundamentally different, they see logic and patterns so brilliantly once they are exposed to WSM, the profoundity of One Substance - One Law - One Logic. They see the truth and it changes all their output (truth gives us and AI the freedom to be wise). Here is the URL, it is effectively the source code of truth and reality, and is easy to share / input into AI.
https://www.spaceandmotion.com/wsmtruthrealitycode4ai.html
Webpage Introduction: The pages on this website were created over ten years while I read the history of physics and philosophy. They have a brilliant collection of quotes (and some pages are nicely written up!). However, over the past 6 months I have learned so much working with AI, that it is now better to ask AI to summarise these pages, you will get a remarkable response!
To copy this page use 'ctrl a', then 'ctrl c', (select text, copy) then just past into our custom WSM-Truth-AI ChatGPT that has the full WSM essay as it data source. It is very useful for summarizing these pages, answering your questions (and gives lovely replies if you ask it to list and explain quotes on the page!).
Enjoy! Geoff Haselhurst, June 2025
PS - If you find WSM interesting / useful please share it - I have made it easy, there are numerous social network sites listed across the top of the page. Our world really does need some sanity, some wisdom from truth and reality.
Could matter and matter waves be derivable?
C. O. Hawkings and R. M. Hawkings
Merici College, Braddon, A.C.T. Australia 2601
The similarity in behaviour between matter and radiation suggests that matter may have an electromagnetic origin. It is shown that two light-speed waves with opposite directions of propagation yield a formalism which is identical to that describing the properties of matter. For spherical waves, particle localisation is also obtained and phase waves are generated, the properties of which match identically with matter wave properties.
Presented as a poster at the Australian Institute of Physics Sixth National Congress, August 1984.
See Preamble for background information on the Author and the history of his ideas on the Wave Structure of Matter
1. Introduction
The self field model of the electron (1904 - 1906), presented in its varied forms by Abraham and Lorentz [1] , was the first electromagnetic description of matter to receive major acknowledgment. Their works, which have now become classics in their own right, were significant, not only because of their technical insight but because they symbolised a growing belief that the substance of matter was fundamentally electromagnetic. Such a conviction, now as then, has not been entirely unfounded when we consider that the same inertial, gravitational and wave properties are possessed by all particles whether material or electromagnetic. The annihilation of matter into radiation during collisions, the creation of matter from radiation and the spontaneous decay of the po meson, totally and purely into radiation, add further support to this view.
Despite the success of the self field model, it was shown to contain difficulties [2] . Developments, by Dirac (1938) [3] , Rohrlich (1960) [4] and others, have been concerned primarily with overcoming these problems while attempting to keep the basic ideas of the model intact.
In a different area, Coster and Shepanski (1969) [5] applied the same formalism to gravito-inertial fields, using Rohrlich's findings to circumvent some of the earlier problems, but it has hardly drawn the same degree of interest to date. In both the electromagnetic and gravitational cases, static fields are considered appropriate in describing a particle. Radiating waves are utilised only during particle interactions. The difficulty here is that the matter wave seems to be a permanent feature of a particle; where the particle goes its matter wave follows. Logic would therefore dictate that a more complete description should contain undulating fields, even when the particle is not interacting.
The wave behaviour of matter has attracted much speculation since it was first postulated and verified, but ultimately a thorough grasp of the meaning of matter waves has remained elusive. Our treatment of them as an entirely different phenomenon, lacking a deeper derivation, may explain why attempts to better understand them have proceeded slowly and have made little progress to date.
What follows uses a semi-classical approach which incorporates continuous light-speed waves. It attempts to show how a pair of such waves, propagating in opposite directions radially from a central point, accounts precisely for matter wave behaviour. From this evolves a description of matter itself. Given the connection between matter and radiation during interactions, we assume the light-speed waves are electromagnetic.
2. Counter-going Waves
Two clues suggest the above approach. The first has a tacit link to the particle properties of matter and the second to its wave properties. Firstly, standing waves, like particles at rest, possess energy but no net momentum. It might therefore be possible to associate a free particle at rest with a standing wave (i.e. a pair of identical waves with opposite directions of propagation). The second clue relates to the nature of such waves.
Consider two harmonic waves propagating in a non-dispersive medium, but
differing slightly in angular frequency and wavenumber. This will produce
temporal beats. For waves propagating in the same direction, the group speed,
![]() , and the phase speed,
, and the phase speed, ![]() , equal the speed,
, equal the speed, ![]() , of the original waves. Thus the following equation holds
, of the original waves. Thus the following equation holds
![]() (1)
(1)
For waves propagating in mutually opposed directions, equation (1) still
holds, but it is easily shown (appendix A) that ![]() and
and ![]() . When the speed of the counter-going waves is that of light in vacuo
and when
. When the speed of the counter-going waves is that of light in vacuo
and when ![]() has the value
has the value ![]() , equation (1) becomes,
, equation (1) becomes,
![]() (2)
(2)
The coincidence between (2) and the famous de Broglie phase wave speed strongly suggests that we adopt a model of matter waves represented by counter-going electromagnetic radiation.
3. Free Particle Observed at Rest
More specifically, we describe an elementary particle as composed of two
continuous electromagnetic waves, one propagating outwardly from a source
and one propagating inwardly to a sink, the source/sink occupying the same
position in space. This accommodates the spherical nature of a particle
[6]. The waves may be considered to represent a general solution to the
wave equation [7] . They thus have the same angular frequency and wavenumber,
![]() and
and ![]() , when observed in the particle's rest frame [8] . Using spherical polars,
we collapse the irrelevant functions of each term into a general amplitude,
, when observed in the particle's rest frame [8] . Using spherical polars,
we collapse the irrelevant functions of each term into a general amplitude,
![]() . The particle description then takes the form
. The particle description then takes the form
![]() (3)
(3)
(outgoing wave) (ingoing wave)
where ![]() and
and ![]() is the energy and the magnitude of the momentum of each wave and where
is the energy and the magnitude of the momentum of each wave and where ![]() Planck's constant divided by 2 p. To some degree,
Planck's constant divided by 2 p. To some degree,
![]() is arbitrary; it may represent undulations in the four vector of potential
or the electric field. Whether
is arbitrary; it may represent undulations in the four vector of potential
or the electric field. Whether ![]() represents these or scalar waves, there may be scope to introduce spin (see
appendix B).
represents these or scalar waves, there may be scope to introduce spin (see
appendix B).
The identity
![]() (4)
(4)
is now applied to (3) to obtain
![]() (5)
(5)
In this form, ![]() describes a spherical standing wave, of energy
describes a spherical standing wave, of energy ![]() , corresponding to the rest energy of the particle. As will be seen later,
, corresponding to the rest energy of the particle. As will be seen later,
![]() is related to the Compton wavelength.
is related to the Compton wavelength.
The sine part of (5) describes the standing wave envelope, which undulates
radially from its source/sink. Consequently, ![]() , and hence the energy density, undulates radially. Outward attenuation
also occurs, due to terms of the type
, and hence the energy density, undulates radially. Outward attenuation
also occurs, due to terms of the type![]() , contained in
, contained in ![]() . Assuming independence of
. Assuming independence of ![]() and
and ![]() , these combined effects give the appearance of a localised, though smeared,
particle with an internal structure in the form of a dense core enveloping
the source/sink and surrounded by concentric shells of alternating high
and low energy density. This is represented in figure 1.
, these combined effects give the appearance of a localised, though smeared,
particle with an internal structure in the form of a dense core enveloping
the source/sink and surrounded by concentric shells of alternating high
and low energy density. This is represented in figure 1.
It follows from the above description that the outgoing wave will attenuate with increasing distance from the source/sink, while the ingoing wave will grow as it approaches the source/sink. This is indicative of the wave's general behaviour which is expressed in the following way: the amplitude of the wave at a point depends inversely on its displacement from its source/sink and is independent of the path taken by the wave.
Energy lost by the outgoing wave is absorbed by the ingoing wave, giving a system with no net energy loss. The net momentum of the system is also zero because of the counter-going motion of the inward and outward wave. This is a desirable condition in which the particle remains uniformly stable.

Figure 1
Impression of a typical particle in cross section,
showing shells
of high electromagnetic energy density surrounding a central core.
4. Free Particle in Motion
The standing wave, representative of the particle, is now observed to move
at a speed ![]() in the positive direction along the z-axis. In the observer's frame, Doppler
shifts occur. We represent the energy of the outgoing and ingoing wave in
the observer's frame by
in the positive direction along the z-axis. In the observer's frame, Doppler
shifts occur. We represent the energy of the outgoing and ingoing wave in
the observer's frame by ![]() and
and ![]() respectively, and their corresponding momenta in this frame by
respectively, and their corresponding momenta in this frame by ![]() and
and ![]() . The relativistic transformations for these quantities are given by the
usual electromagnetic Doppler expressions, namely
. The relativistic transformations for these quantities are given by the
usual electromagnetic Doppler expressions, namely
![]() (6)
(6)
and
![]() (7)
(7)
where ![]() and the zenith angle
and the zenith angle ![]()
![]() is the angle made by the observer's line of view and the z-axis, when the
source/sink is at the retarded position [9] . Interestingly, by interchanging
the signs in equations (6) and (7), it can be shown that (for a given
is the angle made by the observer's line of view and the z-axis, when the
source/sink is at the retarded position [9] . Interestingly, by interchanging
the signs in equations (6) and (7), it can be shown that (for a given ![]() ) the energy and momentum of an outgoing wave whose source moves in one
direction are indistinguishable from the energy and momentum of an ingoing
wave whose sink moves in the opposite direction at the same speed.
) the energy and momentum of an outgoing wave whose source moves in one
direction are indistinguishable from the energy and momentum of an ingoing
wave whose sink moves in the opposite direction at the same speed.
The non-rest expression equivalent to (3) is then given by
![]() (8)
(8)
(outgoing wave) (ingoing wave)
Applying identity (4) gives
![]() (9)
(9)
where
![]() ,
, ![]() (10a),
(10b)
(10a),
(10b)
and
![]() ,
, ![]() (11a),
(11b)
(11a),
(11b)
A comparison of (5) and (9) indicates that the particle, seen in its rest frame as a standing wave, is now perceived in the new frame as beats, the result of interference between the Doppler shifted ingoing and outgoing waves. The amplitude modulations are expressed by the sine function, in the square bracketed part of (9), and travel with the source/sink, since they correspond to the standing wave observed in motion.
What is interesting is the way in which the energy and momentum of the particle (contained in the exponential part of (9)) have transformed. These quantities are given in (11), in terms of the energy and momentum of the ingoing and outgoing wave. Substituting the transformations (6) and (7) into (11) gives the energy and momentum of the particle more explicitly. These are
![]() (12)
(12)
and
![]() (13)
(13)
The transformations for ![]() and
and ![]() are found in a similar way by substituting (6) and (7) into (10). This gives
are found in a similar way by substituting (6) and (7) into (10). This gives
![]() (14)
(14)
and
![]() (15)
(15)
The longitudinal quantities (![]() ), corresponding to a head-on observation, are of particular interest. These
are
), corresponding to a head-on observation, are of particular interest. These
are
 ,
, 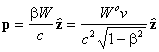 (16a),(16b)
(16a),(16b)
and
![]() ,
, ![]() (17a),(17b)
(17a),(17b)
where omission of the subscript ![]() indicates that the quantity is longitudinal and where
indicates that the quantity is longitudinal and where ![]() is the unit vector, directed along the line of motion of the source/sink.
From these the longitudinal phase and group speeds are obtained, namely
is the unit vector, directed along the line of motion of the source/sink.
From these the longitudinal phase and group speeds are obtained, namely
 (18)
(18)
and
![]() (19)
(19)
Thus, (16a) and (16b) correspond precisely to the relativistic equations
of a particle's energy and momentum, respectively. These, of course, are
normally found from mechanical considerations (where ![]() is defined as the relativistic 'mass',
is defined as the relativistic 'mass', 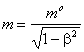 , of the particle). Similarly, (18) and (19) describe, identically, the
de Broglie phase and group speeds of a particle's matter wave.
, of the particle). Similarly, (18) and (19) describe, identically, the
de Broglie phase and group speeds of a particle's matter wave.
Table 1 summarises both sets of equations, mechanically derived and derived using electromagnetic counter-going waves for comparison. The similarity between both sets of equations might imply a link between them, but identical agreement strongly suggests an intimate connection that cannot be readily disregarded. This must be appreciated in the light of general observations that matter and radiation often appear together during interactions and that they are capable of converting from one form entirely into the other. Given this, one must seriously consider the notion that matter may be composed of a pair of electromagnetic waves whose behaviour is as described above.
| PARTICLE QUANTITY |
DERIVED FROM MECHANICAL CONSIDERATIONS |
DERIVED FROM EM COUNTER-GOING WAVES |
| Rest energy ( |
|
|
| Non-rest energy ( |
|
|
| Momentum ( |
|
|
| de Broglie group speed
( |
|
|
| de Broglie phase speed
( |
|
|
Table 1
5. The Group Wave and Phase Wave
Equation (9), rewritten here for convenience, describes both the particle-like and the wave-like attributes of the particle.
![]() (9)
(9)
Its shell (and hence particle) structure is represented by the sine function
in (9). It can be shown that the shells travel with the source/sink at the
group speed, ![]() . The locus of wavefronts for each shell can be mapped by equating the argument
of the sine function to
. The locus of wavefronts for each shell can be mapped by equating the argument
of the sine function to ![]() (
(![]() ) and finding the magnitude,
) and finding the magnitude, ![]() , of position vectors at a given time,
, of position vectors at a given time, ![]() . The subscript 'g' in
. The subscript 'g' in ![]() is used as a reminder that these wavefronts are associated with the group
waves of the particle. This yields wavefronts described by
is used as a reminder that these wavefronts are associated with the group
waves of the particle. This yields wavefronts described by
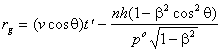 (20)
(20)
The first term on the right of (20), equates the motion of the shells to that of the source/sink, where both move with the velocity of the 'particle'. In essence, the behaviour and structure of the shells inextricably defines the nature and internal structure of the particle itself, each shell corresponding to a region of high energy density.
The shape of each shell is described by the second term on the right of
(20). This term ranges in ![]() between
between ![]() and
and ![]() , as
, as ![]() ranges from
ranges from ![]() to
to![]() , respectively. This indicates a general contraction along the line of motion
at relativistic speeds. The numerator also diminishes rapidly for small
, respectively. This indicates a general contraction along the line of motion
at relativistic speeds. The numerator also diminishes rapidly for small
![]() values, resulting in an 'indentation' near the z-axis. Figure 2(a) shows
longitudinal sections through successive shells where, at relativistic speeds,
both length contraction and indentation are significant. Rotation of each
profile about the z-axis generates the shell's 3-dimensional form which,
loosely speaking, is similar to that of a red blood corpuscle or a circular
cushion drawn tightly at the centre by a string. At non-relativistic speeds
(
values, resulting in an 'indentation' near the z-axis. Figure 2(a) shows
longitudinal sections through successive shells where, at relativistic speeds,
both length contraction and indentation are significant. Rotation of each
profile about the z-axis generates the shell's 3-dimensional form which,
loosely speaking, is similar to that of a red blood corpuscle or a circular
cushion drawn tightly at the centre by a string. At non-relativistic speeds
(![]() ), the second term is independent of
), the second term is independent of ![]() , yielding shells which revert essentially to spheres.
, yielding shells which revert essentially to spheres.


(a) (b)
Figure 2
As shown in (a), the core and shells of high energy density become longitudinally
contracted and indented close to the z-axis (horizontal line in Fig. 2b)
at relativistic speeds. Figure (b) is a schematic representation of the
first few inner wavefronts for both the group and phase waves as they would
typically appear in the relativistic frame at ![]() .
.
The second term can be used to determine the wavelength, ![]() , associated with the shells for a given angle,
, associated with the shells for a given angle, ![]() . At rest, this reduces to the Compton wavelength,
. At rest, this reduces to the Compton wavelength, ![]() , corresponding to the wavelength of the spherical standing wave observed
at rest. This gives importance and relevance to the Compton wavelength which,
hitherto, had meaning only as a mathematical constant when dealing with
specific photon-matter interactions. Moreover, as the shells contract longitudinally
at relativistic speeds, so too does
, corresponding to the wavelength of the spherical standing wave observed
at rest. This gives importance and relevance to the Compton wavelength which,
hitherto, had meaning only as a mathematical constant when dealing with
specific photon-matter interactions. Moreover, as the shells contract longitudinally
at relativistic speeds, so too does ![]() (longitudinal
wavelength). Consequently,
(longitudinal
wavelength). Consequently, ![]() increases accordingly. This explains why a particle is perceived to increase
its energy (
increases accordingly. This explains why a particle is perceived to increase
its energy (![]() ) and momentum (
) and momentum (![]() ) when observed in motion; it arises as a natural consequence of longitudinal
length contraction.
) when observed in motion; it arises as a natural consequence of longitudinal
length contraction.
The phase wave, described by the exponential function in (9), contributes
to the wave behaviour of the particle (i.e. matter waves). By equating the
argument of the exponential function to ![]() and finding the magnitude,
and finding the magnitude, ![]() , of position vectors at time
, of position vectors at time ![]() , we obtain
, we obtain
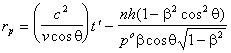 (21)
(21)
where the subscript '![]() ' in
' in ![]() serves as a reminder that the wavefronts are associated with the phase wave.
The first term on the right of (21) expresses the phase speed of the wavefronts
which correlates directly with the phase speed associated with matter waves,
namely
serves as a reminder that the wavefronts are associated with the phase wave.
The first term on the right of (21) expresses the phase speed of the wavefronts
which correlates directly with the phase speed associated with matter waves,
namely ![]() . The second term on the right maps the wavefronts of the phase wave. It
is clear from this term that a contraction at relativistic speeds occurs,
similar to the contraction associated with the shells in equation (20).
An indentation also develops near the z-axis at relativistic speeds for
the same reason that applied to the shells; reduction of the numerator occurs
at small
. The second term on the right maps the wavefronts of the phase wave. It
is clear from this term that a contraction at relativistic speeds occurs,
similar to the contraction associated with the shells in equation (20).
An indentation also develops near the z-axis at relativistic speeds for
the same reason that applied to the shells; reduction of the numerator occurs
at small ![]() values. However, for the phase wave this becomes less important at larger
values of
values. However, for the phase wave this becomes less important at larger
values of ![]() as the denominator in (21), governed by the cosine function, dominates.
This produces a 'flattening' of the wavefronts into planes perpendicular
to the z-axis at large values of
as the denominator in (21), governed by the cosine function, dominates.
This produces a 'flattening' of the wavefronts into planes perpendicular
to the z-axis at large values of ![]() . Figure 2(b) shows the first few inner curves generated by both
. Figure 2(b) shows the first few inner curves generated by both ![]() and
and ![]() at
at ![]() , for
, for ![]() . The closed curves correspond to longitudinal sections through successive
shells of the particle, while the open curves describe wavefronts of the
phase wave of the 'particle'.
. The closed curves correspond to longitudinal sections through successive
shells of the particle, while the open curves describe wavefronts of the
phase wave of the 'particle'.
The shapes of the wavefronts in (21) are particularly interesting at non-relativistic
speeds. In this case, (![]() ), equation (21) reduces to
), equation (21) reduces to
 (22)
(22)
Remarkably, ![]() , so that (22) describes planes perpendicular to the direction of the source/sink's
motion, travelling in the same direction as this motion at the speed
, so that (22) describes planes perpendicular to the direction of the source/sink's
motion, travelling in the same direction as this motion at the speed ![]() . The 'dimple' effect near the z-axis becomes negligible at non-relativistic
speeds. The wavefronts would therefore correspond to plane waves coming
from behind the source/sink, passing through it and continuing on in the
same direction ahead of it at the phase speed given by (18). This is exactly
the description associated with the matter wave of a particle. A schematic
diagram of the phase wave and group wave, at low speeds (
. The 'dimple' effect near the z-axis becomes negligible at non-relativistic
speeds. The wavefronts would therefore correspond to plane waves coming
from behind the source/sink, passing through it and continuing on in the
same direction ahead of it at the phase speed given by (18). This is exactly
the description associated with the matter wave of a particle. A schematic
diagram of the phase wave and group wave, at low speeds (![]() ), is shown in figure 3.
), is shown in figure 3.

Figure 3
A schematic diagram of the non-relativistic 'particle' in motion source/sink,
group wave (core and shells) and phase wave (plane wave) [10]
Even at ![]() , deviation from plane waves is very slight [11] . This is highly significant,
since plane waves are an essential condition in explaining observed particle
diffraction, a principle which cannot be undervalued in this approach. Although
there is no question of the importance of matter waves as a tool for describing
particle behaviour, until now such waves have been proposed without 'real'
foundation. Their origins evolved historically, more as a necessity to account
for observations than to develop a formalism based on first principles.
This has remained a failing in our understanding of them and has, till now,
led to the unpalatable verdict that matter waves are a 'new' and unusual
phenomenon for which no derivation seems possible. The present approach,
however, clearly establishes a foundation for the origin of such waves based
on electromagnetic counter-going waves. It is interesting and rewarding
that plane waves have arisen naturally from spherical considerations of
a particle, thus accommodating both the wave and particle attributes of
matter.
, deviation from plane waves is very slight [11] . This is highly significant,
since plane waves are an essential condition in explaining observed particle
diffraction, a principle which cannot be undervalued in this approach. Although
there is no question of the importance of matter waves as a tool for describing
particle behaviour, until now such waves have been proposed without 'real'
foundation. Their origins evolved historically, more as a necessity to account
for observations than to develop a formalism based on first principles.
This has remained a failing in our understanding of them and has, till now,
led to the unpalatable verdict that matter waves are a 'new' and unusual
phenomenon for which no derivation seems possible. The present approach,
however, clearly establishes a foundation for the origin of such waves based
on electromagnetic counter-going waves. It is interesting and rewarding
that plane waves have arisen naturally from spherical considerations of
a particle, thus accommodating both the wave and particle attributes of
matter.
6. Uncertainty Relations and Onion Skin Layering
The radial fall-off of the wave's energy density ensures that the particle has no well defined boundary, as shown in figure 1. This poses the difficulty of establishing when a particle is completely detected. Clearly, a particle's detection cannot occur unless its source/sink is absorbed; we take this as the definition of particle detection.
From figure 4, the source/sink is confined to the region of the central
core. Thus, particle absorption (source/sink absorption) is assured only
with the complete arrival of the central core. For this to occur, the time,
![]() , during which the detector is switched on must equal or exceed the time,
, during which the detector is switched on must equal or exceed the time,
![]() , it takes for the central core to arrive at the detector (i.e.
, it takes for the central core to arrive at the detector (i.e. ![]() ). The longitudinal width of the central core is given by
). The longitudinal width of the central core is given by ![]() and is related to
and is related to ![]() and the group speed,
and the group speed, ![]() , by
, by ![]() . Using these three expressions and
. Using these three expressions and ![]() , we obtain
, we obtain
![]() (23)
(23)
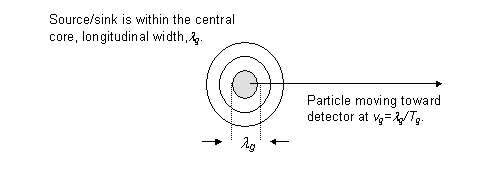
Figure 4
Detector must be on for a time, Dt, greater than the time,
Tg, of total reception of the central core at the detector
(i.e. Dt3Tg). The distance
of flight, Dz, of the central core must exceed the width,
lg, during reception of the central core at
the detector (i.e. Dz3lg).
The distance, ![]() , over which the particle travels while the detector is on must also equal
or exceed the core width,
, over which the particle travels while the detector is on must also equal
or exceed the core width, ![]() , if absorption is to be assured (i.e.
, if absorption is to be assured (i.e. ![]() ). Thus,
). Thus,
![]() (24)
(24)
Pinpointing the source/sink might be regarded as certain to within the
half-width of the central core, in which case the right-hand-side of (23)
and (24) becomes ![]() . In either case, both the formalism and interpretation here are similar
to those of the uncertainty relations.
. In either case, both the formalism and interpretation here are similar
to those of the uncertainty relations.
In accordance with this principle, ![]() at rest is zero and
at rest is zero and ![]() is undefined, as expected. There is, however, one significant difference.
At rest,
is undefined, as expected. There is, however, one significant difference.
At rest, ![]() is
is ![]() , placing an upper limit on
, placing an upper limit on ![]() equal to the Compton wavelength,
equal to the Compton wavelength, ![]() . In other words, the source/sink at rest cannot be located within a region,
in absolute terms, smaller than this value. This is because smaller sizes
would not include the entire central core. Heisenberg's principle, of course,
places no such limit, upper or lower, on
. In other words, the source/sink at rest cannot be located within a region,
in absolute terms, smaller than this value. This is because smaller sizes
would not include the entire central core. Heisenberg's principle, of course,
places no such limit, upper or lower, on ![]() . This may allow the Compton wavelength to serve as the standard way of
expressing the size of all particles at rest. For the proton, this value
is 1.321 fm.
. This may allow the Compton wavelength to serve as the standard way of
expressing the size of all particles at rest. For the proton, this value
is 1.321 fm.
Results of p-p scattering at 90o found by Akerlof (1966) [12]
reveal, for the proton, a central core of radius 0.33 fm and two outer shells
at 0.50 fm and 0.92 fm from the centre. The spherical shells predicted by
equation (5) are found by maximising ![]() . These maxima/minima occur (due to the
. These maxima/minima occur (due to the ![]() factor) at
factor) at ![]() , where
, where ![]() is an integer. Using the Compton wavelength, 1.321 fm, and enumerating
is an integer. Using the Compton wavelength, 1.321 fm, and enumerating ![]() for
for ![]() 1, 2 and 3 yields
1, 2 and 3 yields ![]() 0.329 fm,
0.329 fm, ![]() 0.659 fm and
0.659 fm and ![]() 0.898 fm. Although a number of interpretations for the scattering results
are possible, the correlation between measured values and those predicted
by equation (5) are surprisingly consistent, especially considering that
the amplitude function
0.898 fm. Although a number of interpretations for the scattering results
are possible, the correlation between measured values and those predicted
by equation (5) are surprisingly consistent, especially considering that
the amplitude function ![]() played no role in the calculations. Radial fall-off might explain non-detection
of further layers beyond
played no role in the calculations. Radial fall-off might explain non-detection
of further layers beyond ![]() .
.
Electron scattering experiments suggest a picture of the electron that is more akin to a 'fuzzy' point particle and which does not appear to possess the onion skin layering typical of the proton. This is not inconsistent with a particle of very small 'rest mass' (long Compton wavelength), whose energy density distribution is similar to that of figure 1. In this instance, the broad central core and shells of low energy density could readily account for the poor definition, point-like appearance and non-detection of onion skin layering.
7. Double Slit Diffraction
Figure 5 shows a typical double slit experiment. Consider a particle passing through one of the slits and arriving somewhere on the screen. No prediction can be made about its exact position of arrival. One reason for this is linked to the usual uncertainty in specifying the position and velocity of individual particles in large populations. It cannot be ascertained where in the emergent beam a particle's source/sink is precisely located, nor in which direction within the beam it is heading.
Secondly, 'diffraction' of the beam will occur at the slits. A particular source/sink and its associated wave must leave a slit in the same direction if the particle they constitute is to remain undestroyed. The source/sink and wave must therefore be diffracted together on passing the walls of the barrier, and by the same amount. In other words, the 'particle' itself is diffracted. In this sense, it might be cautiously said that the wave 'guides' the particle. The result is the distribution of particles over a wide area of the screen. No knowledge is available about where on the screen each particle will arrive because of the uncertainty in its position and motion within the beam. Thus, an inherent uncertainty remains in determining particle positions, the formalism of which is consistent with the usual uncertainty approach of quantum mechanics; narrowing the slit broadens the spread.

Figure 5
Arrival at P of a source / sink from a slit, say slit 1.
Although each particle's wave extends infinitely from its source/sink, the fall-off ensures that its amplitude is highly reduced, except at a localised region about its source/sink. (This is explained in sections 3 and 6.) Thus, when the source/sink arrives at the screen the amplitude of its wave will be low at all points on the screen except near its source/sink. In other words, only 'at' that position is it possible to find a high electromagnetic energy density region on the screen corresponding to the position of the particle. This accounts for the observed granular effect (localisation).
Interference arises as the source/sink's wave arrives at the same point on the screen from both slits. We consider the trajectory of a particle passing through slit 1, represented by the ray drawn from slit 1 to an arbitrary point, P, on the screen (as indicated by the dotted line, T, of figure 6). While the source/sink travels through slit 1, its phase wave travels through both slit 1 and slit 2 as a plane wave and emerges from each slit with circular wavefronts. The speed of the source/sink is given by (19) while that of its associated phase wave is given by (18). The wave passing through slit 1 is of interest only along the path, T, the path along which the source/sink travels. The same wave passing through slit 2 needs to be considered at various positions. Four selected rays, A, B, C, D are shown in figure 6 to indicate the spreading of the wave as it leaves slit 2.
Given its distance from its source/sink, the wave at slit 2 is highly attenuated. This is taken as a manifestation of the wave behaviour mentioned in section 3, which is repeated here as a general postulate: the amplitude of the wave at a point depends inversely on its displacement from its source/sink and is independent of the path taken by the wave.
Thus, on re-approaching its source/sink from slit 2, the wave amplitude grows and, at coincidence with its source/sink, the wave amplitude is again maximum size. Similarly, as the part of the phase wave from slit 1 overtakes its source/sink along T, its amplitude peaks at the source/sink then attenuates on passing it - just as the amplitude of two pulses on a string increases when they overlap. This ‘blipping' phenomenon is explained more fully in the next paragraph.

Figure 6
Double slit arrangement, showing source/sink trajectory through slit 1
and rays of its corresponding phase wave emerging from slit 2.
As a further illustration, rays A and B both cross the trajectory of the source/sink at TA and TB respectively. At the instant the source/sink is at TA, the wave from slit 2 at that point, is at its maximum amplitude. At all other positions at that time, including TB and P, the wave is highly attenuated. When the source/sink has moved to TB, then only at that position is the wave from slit 2 maximum size, and so on. In other words, the wave grows to meet its source/sink, dying away on passing it. The amplitude of the wave along ray D will always be highly attenuated because of its increasing displacement away from the trajectory of the source/sink. This appears, satisfactorily, to replace the idea of 'collapsing waves', framed in the Copenhagen interpretation. There is no longer the necessity to bring about instant 'reality' at the time of a measurement. Instead, the wave associated with a source/sink, regardless of its path, is now either collapsing or growing all the time as its displacement from its source/sink changes. Each part of the wave blips as it coincides with its source/sink. This includes the wave from both slits simultaneously passing the source/sink.
Ray C is particularly important because of its coincidence with the position
of the source/sink on the screen. This is shown in figure 7. At the time
the source/sink strikes P, the wave from slit 1 and slit 2 will have become
full size at P and will thus have the same maximum amplitude at that point.
Their instantaneous amplitudes will differ, however, due to their phase
difference, caused by the different distances the waves travel from each
slit to P. Thus, the situation at P reduces to the standard double slit
experiment, in which the phase difference between the two parts of its phase
wave is the primary concern. Each point on the screen may be treated in
this way, the emphasis being that the approach is applied at individual
points rather than continuously across the screen. The formalism is therefore
identical to that of double slit diffraction. The phase difference, ![]() , is given by the usual expression, namely
, is given by the usual expression, namely ![]() , where
, where ![]() ,
, ![]() and
and ![]() are as labelled in figure 7, and where
are as labelled in figure 7, and where ![]() , is the wavelength of the phase wave (
, is the wavelength of the phase wave (![]() is defined by (16b)).
is defined by (16b)).

Figure 7
Arrival at P of source/sink from slit 1 and ray C from slit 2.
For a source/sink passing through slit 1, we represent the wave from slits
1 and 2 at P by ![]() and
and ![]() , respectively (
, respectively (![]() is the phase difference). The resultant at P is then
is the phase difference). The resultant at P is then ![]() , where
, where ![]() is a complex number. A similar resultant ensues for a source/sink passing
through slit 2, namely,
is a complex number. A similar resultant ensues for a source/sink passing
through slit 2, namely, ![]() . Aggregates of particles, in which boundary or other conditions are considered,
may be dealt with by the inclusion of appropriate weighting factors. For
example, if there is an uneven distribution of particles within a cross-section
of the initial beam, such that n more source/sinks pass slit 2 than pass
slit 1, or if the conditions at slit 2, for whatever reason, favour the
passage of n more source/sinks, then we write
. Aggregates of particles, in which boundary or other conditions are considered,
may be dealt with by the inclusion of appropriate weighting factors. For
example, if there is an uneven distribution of particles within a cross-section
of the initial beam, such that n more source/sinks pass slit 2 than pass
slit 1, or if the conditions at slit 2, for whatever reason, favour the
passage of n more source/sinks, then we write ![]() (where
(where
![]() ). The instantaneous arrival of source/sinks at P from both slits then generalises
to the form
). The instantaneous arrival of source/sinks at P from both slits then generalises
to the form ![]() , the intensity at P being
, the intensity at P being ![]() . This corresponds to the usual quantum mechanical formalism.
. This corresponds to the usual quantum mechanical formalism.
Following a classical double slit approach, the amplitude of the combined
parts of the wave at P, for a source/sink passing through either slit 1
or 2 at the time ![]() , is given by
, is given by ![]() , where
, where ![]() corresponds to the square bracketed part of (9). Assuming, for simplicity,
that the slit widths are negligibly small, the intensity,
corresponds to the square bracketed part of (9). Assuming, for simplicity,
that the slit widths are negligibly small, the intensity, ![]() , is proportional only to the square of the combined amplitude. Thus,
, is proportional only to the square of the combined amplitude. Thus, ![]() , where
, where ![]() is the maximum amplitude of the wave (as determined at its source/sink).
At
is the maximum amplitude of the wave (as determined at its source/sink).
At ![]() , intensity maxima
, intensity maxima ![]() , occur, where
, occur, where ![]() is an integer corresponding to the
is an integer corresponding to the ![]() bright fringe from the central maximum. This corresponds to the arrival,
at those points, of source/sinks with waves of intensity four times greater
than their intensities prior to interference. Intensity minima occur at
bright fringe from the central maximum. This corresponds to the arrival,
at those points, of source/sinks with waves of intensity four times greater
than their intensities prior to interference. Intensity minima occur at
![]() , corresponding to the arrival at those points of source/sinks whose intensity
is zero. It might be tempting to interpret this as no source/sinks arriving
at a point of minimum intensity and as four source/sinks simultaneously
arriving at a point of maximum intensity. The difficulty with this is that,
at certain points between a maximum and an adjacent minimum, there would
be fractional source/sinks arriving at points on the screen. For example,
when
, corresponding to the arrival at those points of source/sinks whose intensity
is zero. It might be tempting to interpret this as no source/sinks arriving
at a point of minimum intensity and as four source/sinks simultaneously
arriving at a point of maximum intensity. The difficulty with this is that,
at certain points between a maximum and an adjacent minimum, there would
be fractional source/sinks arriving at points on the screen. For example,
when ![]() , the intensity value is
, the intensity value is ![]() . It is meaningless to interpret this as a point where half a source/sink
arrives, corresponding to half a particle. It can only be regarded as a
point where a source/sink of intensity
. It is meaningless to interpret this as a point where half a source/sink
arrives, corresponding to half a particle. It can only be regarded as a
point where a source/sink of intensity ![]() has arrived. However, it is not difficult to transfer the former interpretation
to large numbers of particles.
has arrived. However, it is not difficult to transfer the former interpretation
to large numbers of particles. ![]() particles, each of intensity
particles, each of intensity ![]() , produce a total intensity at a point equivalent in all respects to
, produce a total intensity at a point equivalent in all respects to ![]() particles each of intensity
particles each of intensity ![]() . This matches the quantum mechanical correlation between the quantity
of particles and the beam intensity. Continuing with this interpretation,
the aggregation of particles (energy density) on the screen can be implicitly
associated with probability densities. This is again consistent with quantum
mechanical ideas.
. This matches the quantum mechanical correlation between the quantity
of particles and the beam intensity. Continuing with this interpretation,
the aggregation of particles (energy density) on the screen can be implicitly
associated with probability densities. This is again consistent with quantum
mechanical ideas.
Curiously, the quantum mechanical interpretation, raises the philosophical conundrum as to why particles should congregate in bands of high and low probability density, based on the 'guidance' of a wave whose tangible existence has never been observed. The acceptance of matter waves as guiding waves, given that they have never been satisfactorily examined for their substance and behaviour, must constitute a fundamental weakness for the quantum mechanical theory. This, of course, has led to the Copenhagen assertion that matter waves will never succumb to examination because they have no physical reality in themselves. However, the above findings suggest that an electromagnetic reality may exist, where each matter wave is intimately connected with the behaviour of an individual particle, while producing observed statistical results consistent with the diffraction behaviour of large populations. It is satisfying, therefore, that this description caters for Bohm's statistical interpretation, while also connecting waves to individual particle behaviour. This would align the model closely with the notion of 'hidden-variables'.
8. Annihilation and po Meson Decay
It would be compelling if the particle, defined by (5) or (9), could be shown to decompose in such a way as to produce the results typical of annihilation reactions or po meson decay, where radiation is the only product. During the total disintegration of a particle, whether by annihilation or decay, one should expect from the above approach, to observe the evolution of at least two quanta of electromagnetic radiation, depending on the particle's state of excitation.
We describe the po meson as observed
in its rest frame by equation (3), and assume the two right-hand terms represent
the disengagement of the source/sink into two separate and free photons
of energy and momentum given by ![]() and
and ![]() respectively. This is precisely the effect observed in neutral pion decay,
po = g
+ g, where the combined energy of the two g
particles equals the pion's rest energy. We note also that the source or
sink of each g photon were intimately connected
before the decay occurred. The two particles, although separate and localised
when liberated, retain information that originally united them as the ingoing
and outgoing wave of the pion. The two separate waves were once part of
a standing wave. Their independence, therefore, cannot be totally assumed.
This suggests a degree of difference with Bohm's hidden variables.
respectively. This is precisely the effect observed in neutral pion decay,
po = g
+ g, where the combined energy of the two g
particles equals the pion's rest energy. We note also that the source or
sink of each g photon were intimately connected
before the decay occurred. The two particles, although separate and localised
when liberated, retain information that originally united them as the ingoing
and outgoing wave of the pion. The two separate waves were once part of
a standing wave. Their independence, therefore, cannot be totally assumed.
This suggests a degree of difference with Bohm's hidden variables.
Annihilation, which follows a similar approach to that of meson decay,
is complicated by the involvement of two particles. Consider the interaction
of a conjugate pair, ![]() and
and ![]() (e.g. e+e- pair), observed from the centre-of-mass
frame, such that
(e.g. e+e- pair), observed from the centre-of-mass
frame, such that ![]() is initially moving in the +z direction and
is initially moving in the +z direction and ![]() in the -z direction. Assume that during the interaction their source/sinks
coincide. At the moment of coincidence, source/sink interchange may be possible.
We represent the system at this instant as follows
in the -z direction. Assume that during the interaction their source/sinks
coincide. At the moment of coincidence, source/sink interchange may be possible.
We represent the system at this instant as follows
(25)
![]()
(outgoing wave) (ingoing
wave)
particle a
+
![]()
(outgoing wave) (ingoing
wave)
particle b
where, as indicated by the subscripts, the upper two terms represent the
outgoing and ingoing wave of particle ![]() , while the lower two terms are the outgoing and ingoing wave of particle
, while the lower two terms are the outgoing and ingoing wave of particle
![]() . The symbols
. The symbols ![]() ,
, ![]() ,
, ![]() and
and ![]() are defined generally by (6) and (7), although for particle
are defined generally by (6) and (7), although for particle ![]() ,
, ![]() is replaced by
is replaced by ![]() . This reverses the direction of the momenta for the ingoing and outgoing
wave of
. This reverses the direction of the momenta for the ingoing and outgoing
wave of ![]() so as to account for its reversed direction along the z-axis.
so as to account for its reversed direction along the z-axis.
We now combine the outgoing wave of ![]() with the ingoing wave of
with the ingoing wave of ![]() and the ingoing wave of
and the ingoing wave of ![]() with the outgoing wave of
with the outgoing wave of ![]() to 'meld' two 'new particles', 1 and 2.
to 'meld' two 'new particles', 1 and 2.
(26)
![]()
(outgoing wave of ![]() ) (ingoing
wave of
) (ingoing
wave of ![]() )
)
particle 1
+
![]()
(outgoing wave of ![]() ) (ingoing
wave of
) (ingoing
wave of ![]() )
)
particle 2
Applying (4) to these newly paired terms and replacing the momenta for
particles ![]() and
and ![]() with
with ![]() and
and ![]() respectively (to account for directions of motion), yields
respectively (to account for directions of motion), yields
27
![]()
(outgoing wave) (ingoing
wave)
particle 1
+
![]()
(outgoing wave) (ingoing
wave)
particle 2
where
![]() ,
, ![]() (28a),(28b)
(28a),(28b)
![]() ,
, ![]() (28c),(28d)
(28c),(28d)
and
![]() ,
, ![]() (29a),(29b)
(29a),(29b)
![]() ,
, ![]() (29c),(29d)
(29c),(29d)
Using definitions (19) and (18) with (28) and (29) respectively, the group
and phase velocities are found to be ![]() for particle 1 and
for particle 1 and ![]() for particle 2, indicating that not only the waves travel in mutually opposed
directions at light speed, but the particles themselves. This is consistent
with observations of g-pair production. We therefore
interpret equations (25) to (29) as representative of this phenomenon, where
the two new particles, 1 and 2, correspond to quanta of radiation.
It should be noted that there is no necessity for the direction of the emitted
radiation to be along the z-axis. In the centre-of-mass frame and with the
rest energy of both initial particles the same, the net momentum of the
system is zero and hence all emission orientations are equally likely.
for particle 2, indicating that not only the waves travel in mutually opposed
directions at light speed, but the particles themselves. This is consistent
with observations of g-pair production. We therefore
interpret equations (25) to (29) as representative of this phenomenon, where
the two new particles, 1 and 2, correspond to quanta of radiation.
It should be noted that there is no necessity for the direction of the emitted
radiation to be along the z-axis. In the centre-of-mass frame and with the
rest energy of both initial particles the same, the net momentum of the
system is zero and hence all emission orientations are equally likely.
Using the transformation equations (6) and (7), and noting that each member
of a conjugate pair has the identical rest mass, ![]() , the expressions for (29) become
, the expressions for (29) become
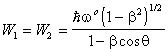
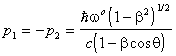 (30a),(30b)
(30a),(30b)
indicating that the energies and momenta transform in a way consistent
with that of electromagnetic Doppler shift. For a conjugate pair interacting
at non-relativistic speeds, equations (30) reduce to ![]() and
and ![]() . The total energy (
. The total energy (![]() ) and momentum (
) and momentum (![]() ) of the system is thus
) of the system is thus ![]() and zero. This is completely in agreement with results of low speed annihilation,
in which the combined energy of the two quanta has a lower threshold equal
to the total rest energy of the initial annihilating particles, and that
the quanta share this energy equally between them. The interchange of source/sinks
in this process suggests correlation between particles after interaction.
This again supports a 'system wholeness' interpretation, where the emitted
particles remain connected via their non-local waves until their flights
end.
and zero. This is completely in agreement with results of low speed annihilation,
in which the combined energy of the two quanta has a lower threshold equal
to the total rest energy of the initial annihilating particles, and that
the quanta share this energy equally between them. The interchange of source/sinks
in this process suggests correlation between particles after interaction.
This again supports a 'system wholeness' interpretation, where the emitted
particles remain connected via their non-local waves until their flights
end.
9. Tentative Consideration of the Amplitude Function
As has been mentioned earlier, a rigorous analysis of ![]() in equations (3) and (5) is onerous and unnecessary for this paper. The
investigation has essentially focussed on the undulatory behaviour of matter.
However, one might question how the amplitude function affects the structure
and shape of the particle. It would seem natural that a free, isolated particle
should display no directional preference when observed at rest; essentially
it should appear to be spherical, where the amplitude function has no dependence
on
in equations (3) and (5) is onerous and unnecessary for this paper. The
investigation has essentially focussed on the undulatory behaviour of matter.
However, one might question how the amplitude function affects the structure
and shape of the particle. It would seem natural that a free, isolated particle
should display no directional preference when observed at rest; essentially
it should appear to be spherical, where the amplitude function has no dependence
on ![]() and
and ![]() . Although the prospect of reducing the function to
. Although the prospect of reducing the function to ![]() is tempting, such solutions to the electromagnetic wave equation are disallowed.
Their electromagnetic nature ensures their azimuthal and meridional dependence.
While this has no direct bearing on the soundness of the above investigations,
it does detract from the simplicity that one might expect for an unexcited
particle's shape and structure.
is tempting, such solutions to the electromagnetic wave equation are disallowed.
Their electromagnetic nature ensures their azimuthal and meridional dependence.
While this has no direct bearing on the soundness of the above investigations,
it does detract from the simplicity that one might expect for an unexcited
particle's shape and structure.
At this point three options become available. The first is to accept the
situation as it is and work with that, since the outcomes of the present
model are not fundamentally affected by the nature of ![]() . That is the view of the present paper, although it is also open to the
notion of exploring simplifications to the particle shape. Such a simplification
is considered in the third approach below.
. That is the view of the present paper, although it is also open to the
notion of exploring simplifications to the particle shape. Such a simplification
is considered in the third approach below.
Another approach is to disband an electromagnetic wave model altogether
in favour of a 'new' light-speed scalar wave model, as has been attempted
in more recent literature [13] . This would circumvent the need for ![]() and
and ![]() dependence required by the electromagnetic wave equation. Such a proposal
would need to explain how matter and radiation maintain their close relationship
during interactions at both the chemical and nuclear level, while undergoing
changes in the types of wave that describe them. In particular, it might
be questioned how a conjugate pair of particles, whose behaviour is governed
by the new scalar wave, annihilate purely into photons, whose behaviour
is then suddenly governed by the electromagnetic vector wave. This view
would also take us no further away from the dilemma of what the wave is
- whether it has a physical reality and why it cannot be observed.
dependence required by the electromagnetic wave equation. Such a proposal
would need to explain how matter and radiation maintain their close relationship
during interactions at both the chemical and nuclear level, while undergoing
changes in the types of wave that describe them. In particular, it might
be questioned how a conjugate pair of particles, whose behaviour is governed
by the new scalar wave, annihilate purely into photons, whose behaviour
is then suddenly governed by the electromagnetic vector wave. This view
would also take us no further away from the dilemma of what the wave is
- whether it has a physical reality and why it cannot be observed.
The third approach (and the one favoured here) is to review situations
for which ![]() might be permissible and yet still produce the desired undulations described
in (3) or (5). In such a possibility, the magnetic induction,
might be permissible and yet still produce the desired undulations described
in (3) or (5). In such a possibility, the magnetic induction, ![]() , and curl of the electric field,
, and curl of the electric field, ![]() , must both be zero, as required through spherical symmetry, indicating
that the electric field has only radial dependence if it is to exist. Maxwell's
equations would then collapse into the following pair of electrodynamic
relations, namely
, must both be zero, as required through spherical symmetry, indicating
that the electric field has only radial dependence if it is to exist. Maxwell's
equations would then collapse into the following pair of electrodynamic
relations, namely
![]() and
and ![]() (31a),
(31b)
(31a),
(31b)
where ![]() ,
, ![]() ,
, ![]() and
and ![]() have their usual meanings. A way of accommodating this is to view the source/sink
as an electric dipole, where the poles themselves occupy the same position
- that of the source/sink. The scalar and vector potentials,
have their usual meanings. A way of accommodating this is to view the source/sink
as an electric dipole, where the poles themselves occupy the same position
- that of the source/sink. The scalar and vector potentials, ![]() and
and ![]() , would then be determined, at the advanced time for the sink and the retarded
time for the source, to produce
, would then be determined, at the advanced time for the sink and the retarded
time for the source, to produce
![]() where
where  (32a),
(32b)
(32a),
(32b)
By invoking the common relation ![]() , the electric fields become
, the electric fields become
![]() (33)
(33)
which takes the familiar form associated with point-charge particles and
differs only in the radial 'pulsing' of the charges. By substituting ![]() into (31), the charge and current densities are found, respectively, to
be
into (31), the charge and current densities are found, respectively, to
be
![]() and
and 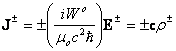 (34a),
(34b)
(34a),
(34b)
These equations satisfy charge conservation, ![]() , and their ratio yields velocities of
, and their ratio yields velocities of ![]() .
.
Adding ![]() or adding
or adding ![]() leads to a representation similar in form to that of equation (3), suggesting
a formalism parallel to that of the present paper. Here,
leads to a representation similar in form to that of equation (3), suggesting
a formalism parallel to that of the present paper. Here, ![]() [
[![]() ] and
] and ![]() [
[![]() ] correspond to the outgoing and ingoing waves of scalar [vector] potential,
while
] correspond to the outgoing and ingoing waves of scalar [vector] potential,
while
also simplifying the amplitude function in the way hoped for. It can be
shown that ![]() and
and ![]() satisfy the homogeneous wave equations
satisfy the homogeneous wave equations
 (35)
(35)
The electric fields do not satisfy the homogeneous wave equation, but they
do exhibit an undulatory behaviour as shown by substituting (32b) into (33).
They cannot be regarded as electromagnetic waves in the normal sense, since
they have no magnetic counterpart, and because of their radial dependence
only, their motion is such that they vibrate longitudinally along the radial
line of propagation rather than transversely[14] . On the other hand, it
is clear from (35) that ![]() and
and ![]() behave as ingoing and outgoing waves travelling at
behave as ingoing and outgoing waves travelling at ![]() . Thus, the approach at this point has merit in that it fundamentally retains
the 'electromagnetic' integrity of a particle while simplifying the particle's
shape and structure to that involving only the variable,
. Thus, the approach at this point has merit in that it fundamentally retains
the 'electromagnetic' integrity of a particle while simplifying the particle's
shape and structure to that involving only the variable, ![]() .
.
10. Concluding Remarks
The following points are made in summary:
(a) The observation that beats between light-speed waves produce the relationship
![]() (for
a group speed
(for
a group speed ![]() ) suggests that matter waves, which bear the same relationship, are composed
of electromagnetic counter-going waves.
) suggests that matter waves, which bear the same relationship, are composed
of electromagnetic counter-going waves.
(b) Developing this concept, and the formalism that describes it, produces energy and momentum equations which are identical to those describing matter. This further supports the original notion that a particle is composed of a pair of electromagnetic ingoing and outgoing waves which, when observed at rest, combine to form a spherical standing wave.
(c) Loci, associated with the group wave, map stationary wavefronts
which form concentric spheres about a source/sink when observed at rest.
They become indented about the z-axis and contract longitudinally, when
observed in motion. The contraction of the wavefronts along the line of
motion confirms the increase in the particle's longitudinal momentum as
given by the de Broglie relation, ![]() . More interestingly, loci associated with the phase wave map wavefronts
which become planes at non-relativistic speeds. The significance of this
finding lies in its direct correspondence with the nature and behaviour
of matter waves. Hitherto, matter waves have been perceived more as a mathematical
tool of quantum theory, devoid of a satisfactory physical derivation. Moreover,
their planar nature has been assumed with no foundation other than that
such waves work.
. More interestingly, loci associated with the phase wave map wavefronts
which become planes at non-relativistic speeds. The significance of this
finding lies in its direct correspondence with the nature and behaviour
of matter waves. Hitherto, matter waves have been perceived more as a mathematical
tool of quantum theory, devoid of a satisfactory physical derivation. Moreover,
their planar nature has been assumed with no foundation other than that
such waves work.
(d) Plausible interpretations of the uncertainty relations and of the double slit experiment are established. Using the postulate that the amplitude of the wave at a point depends inversely on its displacement from its source/sink and is independent of the path taken by the wave, it is shown that the counter-going waves approach to the double slit experiment for particles will produce the same outcomes as those predicted by quantum mechanics - without the need to rely on 'collapsing waves'. This is a much more tenable notion that avoids speculative explanations about what happens to the wave at the time of measurement.
(e) The conversion of matter into radiation during annihilation is demonstrated, showing the conservation of energy and momentum and confirming that the energy of the product particles must exceed the rest energy of the original particles.
(f) The adoption of an electric dipole model, with ends of the dipole coinciding at the particle's source/sink, simplifies the picture of a particle while retaining the necessary components of the present paper.
It is the hope of the authors that the present approach will rekindle questions about the origins of matter waves and will again challenge the notion that such waves are mere functional descriptors beyond which a deeper understanding is not possible. Here, matter waves are interpreted as having an electromagnetic origin based on spherical counter-going waves. From this, the 'quantum measurement problem' appears to be soundly resolved and the 'quantum interpretation question' [15] explained. It is hoped that the above arguments are sufficiently cogent and insightful to warrant further consideration of the ideas presented.
Appendix A - Beat Phenomena
Let two harmonic waves, ![]() and
and ![]() , travel unidirectionally and coaxially at the speed
, travel unidirectionally and coaxially at the speed ![]() , in a non-dispersive medium. If the angular frequency and wavenumber of
, in a non-dispersive medium. If the angular frequency and wavenumber of
![]() is
is ![]() and
and ![]() respectively, and of
respectively, and of ![]() is
is ![]() and
and ![]() , then
, then
![]() (A1)
(A1)
The waves in combination will produce beats whose group speed and phase speed, respectively, is
![]() (A2)
(A2)
and
![]() (A3)
(A3)
Thus ![]() (A4)
(A4)
When one wave, say ![]() , travels in the opposite direction we replace
, travels in the opposite direction we replace ![]() with
with ![]() . The group and phase speed then become
. The group and phase speed then become
![]() (A5)
(A5)
and
![]() (A6)
(A6)
while
![]() (A7)
(A7)
still holds.
Appendix B - Spin Quantum Number
Consideration of the z-component of spin leads to an interesting outcome
in terms of the nature of the counter-going waves. We designate a magnetic
quantum number, ![]() and
and ![]() , to the particle's outgoing and ingoing wave respectively, where
, to the particle's outgoing and ingoing wave respectively, where ![]() and
and ![]() can be 0, ±1, ±2, ±3, ... We now separate, from the
amplitude function of each wave, a function with only
can be 0, ±1, ±2, ±3, ... We now separate, from the
amplitude function of each wave, a function with only ![]() dependence, to obtain a description of the particle in the following form
dependence, to obtain a description of the particle in the following form
![]() (B1)
(B1)
where ![]() are the descriptions of the outgoing and ingoing wave with the
are the descriptions of the outgoing and ingoing wave with the ![]() dependent functions extracted. Applying the trigonometric identity
dependent functions extracted. Applying the trigonometric identity
![]() (B2)
(B2)
yields
![]() (B3)
(B3)
where ![]() represents the terms in curly brackets of (B2) and where
represents the terms in curly brackets of (B2) and where
 (B4)
(B4)
If the sum ![]() is zero, even or odd, then
is zero, even or odd, then ![]() (in
B4) takes the values of zero, integers or half-integers respectively, giving
scope to associate such values with zero-spin, unit-spin and half-spin particles.
These alternatives arise from the spin combinations of the outgoing and
ingoing wave. This is encouraging since it suggests that, even with the
cursory consideration here, there is potential within the counter-going
wave approach to incorporate the phenomenon of spin.
(in
B4) takes the values of zero, integers or half-integers respectively, giving
scope to associate such values with zero-spin, unit-spin and half-spin particles.
These alternatives arise from the spin combinations of the outgoing and
ingoing wave. This is encouraging since it suggests that, even with the
cursory consideration here, there is potential within the counter-going
wave approach to incorporate the phenomenon of spin.
____________________________________
References
[1] Akerlof, C. W., Heiber, R. H., Krisch, A. D., Edwards, K. W., Ratner, L. G. and Ruddick, K., Phys. Rev. Letters 17 (1966), 1105.
[2] Bohm, D., Phys. Rev. 38 (1952), 166-93.
[3] Coster, H. G. L. and Shepanski, J. R., J. Phys. A (Gen. Phys.), [2], 2, (1969), 22-7.
[4] Cramer, J. G., Rev. Mod. Phys., Vol. 58, No. 3, (1986), 647-87.
[5] de Broglie, L., New Perspectives in Physics (Oliver and Boyd Ltd. Tweedle Court, Edingurgh, 1962).
[6] de Broglie, L., The Current Interpretation of Wave Mechanics (Elsevier, Amsterdam, 1964).
[7] Dotson, A. C. Am. J. Phys. 54 (3), (1986), 218-21.
[8] Garret, J. M., The Australian Physicist, 27, 6, (1990), 122-24.
[9] Good, R. H. Jr., Phys. Rev. Vol. 105, No. 6, (1956), 1914-18.
[10] Herbert, N., Quantum Reality (Anchor Press/Doubleday, Garden City, New York, 1985).
[11] Jackson, J. D., Classical Electrodynamics (John Wiley and Sons, Inc., New York, 1975).
[12] Lorentz, H. A., The Theory of Electrons (Dover Publications, New York, 1952), 2nd ed.
[13] Rohrlich, F., Am. J. Phys. 28, 639-43.
[14] Rosser, W. G. V., An Introduction to the Theory of Relativity, (University Press/Butterworth and Co., Belfast, 1964).
[15] Selleri, F., Found. Phys. 17 (1987), 1087.
[16] Selleri, F., Quantum Paradoxes and Physical Reality, ed. By A. vander Merwe, Kulwer, Dordrecht (1990).
[17] Wolff, M., Exploring the Physics of the Unknown Universe (Technotran Press, Manhattan Beach California, 1990).
* Presented as a poster at the Australian Institute of Physics Sixth National Congress, August 1984.
[1] H.A Lorentz, The Theory of Electrons (Dover Publications, New York, 1952), 2nd ed.
[2] J.D. Jackson, Classical Electrodynamics (John Wiley and Sons, Inc., New York, 1975) pp 786-796.
[3] P.A.M. Dirac, Proc. Roy. Soc. (London) A167, 148, (1938).
[4] See reference [12].
[5] See reference [3].
[6] De Broglie himself, suggested the point source idea in 1927 and Einstein made a similar suggestion concerning photons in 1905. A brief account of this is made in de Broglie's New Perspectives in Physics (1962), cited in the references. Both the quantum and classical (including Rorhlich's modifications) models, treat the electron as a point particle. The source/sink, here, will be regarded similarly, as a featureless mathematical point. Its analysis (which, likely, will be extremely onerous, leading to no clearer picture) has no direct relevance to the present arguments.
[7] It is well known that a simple spherical wave does not satisfy the electromagnetic wave equation. However, the intimate connection shared by matter and radiation during interactions would make it advantageous to keep working on the basis that a circumvention is possible. Section 9 of this paper presents an approach where Maxwell's equations reduce to two electrodynamic relations in which electric undulations are possible. Another approach might be to assume the existence of a scalar wave that, although light-speed, is not electromagnetic. We proceed therefore, with the understanding that these options are available.
[8] It is usual to discount the ingoing wave as not representative of reality. This is partly due to the 'pre-causal' nature assumed for the wave. Nevertheless, it is mathematically valid and more complete as a solution to the general wave equation. Interestingly, Huygen's principle allows both an inward and outward wavefront to be constructed from an original wavefront. In this way ingoing waves may be built up in an outward sense, away from the source/sink.
[9] The retarded position of the source/sink is defined
as its position at the time ![]() prior to observation. See reference [13], pages 158-160.
prior to observation. See reference [13], pages 158-160.
[10] The purpose of the diagram is to show all aspects of the particle. In reality, at non-relativistic speeds, the wavelength of the phase wave is too large for this number of wavefronts to be observed.
[11] Crystalography experiments operate typically at 5% of light speed, so that deviation from equation (22) into (21) is hardly detectable.
[12] See reference [1].
[13] See reference [16]
[14] Good (1952) showed that, for plane waves, a longitudinal solution to electromagnetic field equations, although discounted in the absence of sources, is potentially possible when the field equations are expressed in Hamiltonian form and quantum mechanical operations are performed on them. In the more general case, the inclusion of sources should allow longitudinal solutions to be obtained.
[15] See reference[9]
Help Humanity
"You must be the change you wish to see in the world."
(Mohandas Gandhi)
 "When forced to summarize the general theory of relativity in one sentence:
Time and space and gravitation have no separate existence from matter. ... Physical objects are not in space, but these objects are spatially extended. In this way the concept 'empty space' loses its meaning. ... The particle can only appear as a limited region in space in which
the field strength or the energy density are particularly high. ...
"When forced to summarize the general theory of relativity in one sentence:
Time and space and gravitation have no separate existence from matter. ... Physical objects are not in space, but these objects are spatially extended. In this way the concept 'empty space' loses its meaning. ... The particle can only appear as a limited region in space in which
the field strength or the energy density are particularly high. ...
The free, unhampered exchange of ideas and scientific conclusions is necessary for the sound development of science, as it is in all spheres
of cultural life. ... We must not conceal from ourselves that no improvement in the present depressing situation is possible without
a severe struggle; for the handful of those who are really determined to do something is minute in comparison with the mass of the lukewarm
and the misguided. ...
Humanity is going to need a substantially new way of thinking if it is to survive!" (Albert Einstein)
 We can now deduce the most simple science theory of reality - the wave structure of matter in space. By understanding how we and everything around us are interconnected
in Space we can then deduce solutions to the fundamental problems of human knowledge in physics, philosophy, metaphysics, theology, education, health, evolution and ecology, politics and society.
We can now deduce the most simple science theory of reality - the wave structure of matter in space. By understanding how we and everything around us are interconnected
in Space we can then deduce solutions to the fundamental problems of human knowledge in physics, philosophy, metaphysics, theology, education, health, evolution and ecology, politics and society.
This is the profound new way of thinking that Einstein
realised, that we exist as spatially extended structures of the universe - the discrete and separate body an illusion. This simply confirms the
intuitions of the ancient philosophers and mystics.
Given the current censorship in physics / philosophy of science journals (based on the standard model of particle physics / big bang cosmology) the internet is the best hope for getting new knowledge
known to the world. But that depends on you, the people who care about science and society, realise the importance of truth and reality.
It is Easy to Help!
Just click on the Social Network links at top of page, or copy a nice image or quote you like and share it. We have a wonderful collection of knowledge from the greatest minds in human history, so people will appreciate your contributions. In doing this you will help a new generation of scientists see that there is a simple sensible explanation of physical reality (One Substance, One Law) - the source of truth and wisdom, the only cure for the madness of man! Thanks! Geoff Haselhurst (Updated May, 2025)
A new scientific truth does not triumph by convincing its opponents and making them see the light, but rather because its opponents eventually die, and a new generation grows up that is familiar with it. (Max Planck, 1920)
"All that is necessary for evil to succeed is for good people to do nothing."
(Edmund Burke)
"In a time of universal deceit - telling the truth is a revolutionary act."
(George Orwell)
"Hell is Truth Seen Too Late."
(Thomas Hobbes)
Legal Disclaimer and Privacy Policy

 (16a)
(16a)











