---

The Wave Structure of Matter (WSM)
One Substance - One Law - One Logic

---

"Behind it all is surely an idea so simple, so beautiful, that when we grasp it we will all say to each other, how could it have been otherwise? How could we have been so stupid?" (Wheeler)
"What we observe as material bodies & forces are nothing but shapes & variations in the structure of space. Subject & object are one." (Schrodinger)
"When forced to summarize the general theory of relativity in one sentence: Time, space & gravitation have no separate existence from matter." (Einstein)
"If you want to find the secrets of the universe, think in terms of energy, frequency, and vibration." (Tesla)

---

---

---

---

On the Geometric Physical Foundations of
Euler's Equation

"There is a famous formula — perhaps the most compact and famous of all formulas — developed by Euler from a discovery of De Moivre: e^iπ + 1 = 0. Elegant, concise, and full of meaning … It appeals equally to the mystic, the scientist, the philosopher, the mathematician." (Edward Kasner)

"Gentlemen, that is surely true, it is absolutely paradoxical; we cannot understand it, and we don't know what it means. But we have proved it, and therefore we know it must be the truth." (Benjamin Peirce)

"The mathematician plays a game in which he himself invents the rules while the physicist plays a game in which the rules are provided by nature, but as time goes on it becomes increasingly evident that the rules which the mathematician finds interesting are the same as those which nature has chosen." (Paul Dirac)

Introduction

There is an intriguing mystery about this fundamental natural constant, e, Euler's number - about its foundations, and its almost magical power. Below I present a remarkably simple geometric solution to this mystery, relating not only to Euler's number e, but to mathematics and its connection to geometry and thus to physical reality itself.

I know these are extraordinary claims, but what follows is extraordinary - the solution is so simple and obvious, so profound in connecting geometry and mathematics with physical reality (the aim of mathematical physics).

To explain this solution we must simply consider e in relation to Pi (two fundamental natural constants).
They are both irrational, transcendental numbers, both central to mathematics and physics.
Pi has the simple obvious geometric foundation, the ratio of the circumference C to diameter D of a circle. Thus it would be reasonable to expect e to have some fundamental geometric meaning too.
But it doesn't!
In fact e was first discovered by calculating compound interest (Bernoulli, Euler), which reflects one unique property of e relating to continuous growth - its growth determines its size, and its size determines its growth (its growth continuously determines its future growth). This is represented mathematically as the derivative of e^x = e^x.
The value of e is most commonly calculated using either the limit of (1 + 1/n)ⁿ as n approaches infinity, or the sum of an infinite series of 1/n factorial.

We see, that compared to Pi, e seems infinitely complicated (we discuss infinity below when we consider the accuracy of infinitesimal calculus).

 

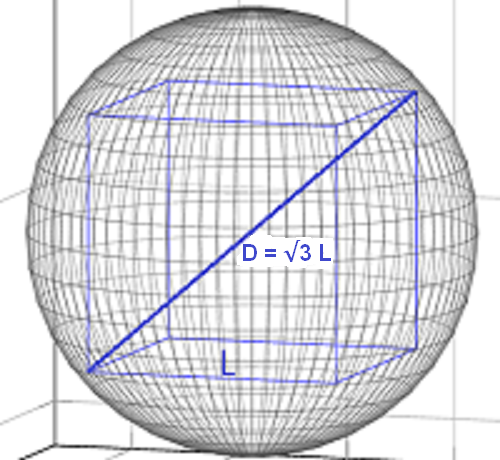
Geometric Solution

So let us now consider the geometric solution, the beautiful simplicity of geometry derived from physical reality that gives rise to e.

All we had to do was transform the one dimensional (length) geometry of circles and lines into three dimensional (volume) geometry of spheres and cubes.

When we apply this three dimensional transformation to Pi, we transform from the ratio of a line enclosed within a circle, to a cube enclosed within a sphere, where the ratio of the volume of the sphere to the volume of the cube is the three dimensional equivalent of Pi.

So now for the fun part. Using just simple high school maths we can deduce the most remarkable relationships.

We begin by applying Pythagoras' theorem to the enclosed cube (with edges length L) to calculate the diagonal length D = √3 L. This must equal the diameter (D) of the sphere enclosing the cube, thus connecting the cube and the sphere both physically and mathematically (a three dimensional equivalent of trigonometry).

Diagonal = Diameter D = √3 L.

Radius r = D/2 = √3/2 L.

Thus r/L = √3/2

This ratio of √3/2 is a most profound transformation, converting from one dimension to three dimensions, from a cube to a sphere.

So now let us apply this 3D transformation of √3/2 to Pi.

As we have said, this transforms the length ratio of a line enclosed in circle, Pi, to the volume ratio of a cube enclosed within a sphere. We find that the ratio, symbolized with brackets around e, what I will call geometric (e) equals;

This is remarkably similar to Euler's number e = 2.7182818284

As a ratio (e)/e = 1.0008892447

It is here worth pausing and thinking how remarkable this is, to get a number so close to e when transforming Pi to three dimensions. Equally remarkable, that no one ever thought to do this until now. (It also leads me to think that infinitesimal calculus used to calculate e is giving us very precise approximations, but not the true value, this is discussed below.)

To confirm that the ratio of the volume of a sphere to the cube enclosed within it is √3/2 Pi = (e) we can use the well known equation for the volume of a sphere.

Volume of Sphere Vs = 4/3 Pi r³

Substitute r = √3/2 L

Volume of Sphere Vs = 4/3 Pi (√3/2 L)³ = √3/2 Pi L³ = (e) L³

Volume of Cube Vc = L³

Volume of Sphere over volume of Cube Vs/Vc = (e) L³ / L³ = (e)

Thus merely being logical and sensible in exploring this three dimensional transformation of Pi, we get this number √3/2 Pi that is so enticingly close to Euler's e such that (e)/e = 1.0008892447.

This should excite any mathematician, physicist, or philosopher.

Let us now consider three remarkable things about this ratio of r/L = √3/2

i) The 4/3 is canceled by the (√3/2)³ leaving √3/2, strongly suggesting that this ratio of √3/2 is correctly connected to the volume of the sphere (geometry) and physical reality.

ii) It is the only value of r that causes the volume of the sphere 4/3 Pi r³ to equal half the circumference Pi r which equals (e).
This connection between (e) and the volume of the sphere and rotation around the circle becomes important when we consider Schrodinger's wave equation, which uses e to generate rotating waves to explain de Broglie waves and the discrete energy of light 'quanta' (matter is treated as a wave, thus the electrons can only exist in discrete orbits that have allowed standing waves).

iii) When the length and thus the volume of the cube is 1, then the radius is √3/2. This proves to be very important when we later consider waves with wavelength of 1, and transforming three orthoganal plane waves (cube with L = 1, volume = 1) to a spherical standing wave (sphere with r = √3/2, volume = (e)), and how this also connects mathematics, geometry and physical reality.

I would like to again emphasise how odd it is that no one ever did this, to transform Pi to three dimensions - this was always an obvious thing to explore - we experience reality in three dimensions.
This is not trivial, I taught this mathematics when I was much younger, and it is only 40 years later that this finally orrurred to me, and it came from considering the wave nature of the Schrodinger and Euler equations (discussed below). My conclusion is that pre-existing ideas can completely blind us to simple obvious truths, and this is why novel truths are often discovered by individuals outside the system. (Yes, I am a natural philosopher, I live in Nature, outside the system.)

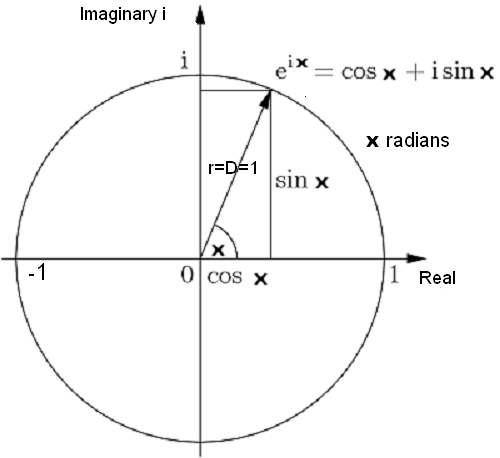
i) Trigonometry uses a similar relationship on a two dimensional plane, uniting the diagonal of a rectangle D (thus the hypotenuse of a right triangle) with the radius of a unit circle r, where D=r=1. (See diagram on right.)

ii) We use the units of cubic meters for volume, yet we know that matter interacts spherically, thus transforming from a cube to a sphere (which (e) does) is central to reality. This is why the equation for a sphere, Pythagoras theorem, and Einstein's metric are all the same fundamental relationship (see diagram on right and quote below, I discuss this in detail in the lower section on Euler's equation). "From the latest results of the theory of relativity it is probable that our three dimensional space is also approximately spherical, that is, that the laws of disposition of rigid bodies in it are not given by Euclidean geometry, but approximately by spherical geometry. ... The defining equation of the metric dx2 + dy2 + dz2 =(c dt)2 is then nothing but the Pythagorean theorem applied to the differentials of the co-ordinates." (Albert Einstein)

 

Let's now consider more of the properties of a cube enclosed within a sphere (see table below), comparing the relationships between the cubic geometry of (e) and L, and the spherical geometry of Pi and r.

I also include the exact results for two special cubes / spheres, where L=1, and thus r = √3/2, and where r=1 and L = 2/√3. In the final section on waves we discuss what happens when we have set wavelength = L = 1. The results are most interesting!

Finally, the table shows the derivatives, their physical meaning is obvious. The area of a circle = Pi r², its derivative, the circumference = 2pi r (the area of a circle changes by its circumference), and likewise for a sphere the volume = 4/3 Pi r³ and its derivative, the surface area = 4pi r² (the volume of a sphere changes by its surface area).

Object	Cube (e,L)	Ratio	Sphere (Pi,r)	L=1, r=√3/2	r=1, L=2/√3
Volume of Sphere (Vs)	(e)L3	=	4/3 Pi r3	(e)	4/3 Pi
Volume of Cube (Vc)	L3	=	(2/√3)3r3	1	(2/√3)3
Ratio Vs / Vc	(e)	=	(e)	(e)	(e)
Derivative (Vs)	3(e)L2	* Pi/(e) =	4 Pi r2	3(e)	4 Pi
Derivative (Vc)	3L2	* Pi/(e) =	(2/√3)4r2	3	4(2/√3)
Ratio Derivative Vs / Vc	(e)	=	(e)	(e)	(e)

The two colored rows show the ratio of Vs / Vc, and their derivatives. And you get this beautiful row of (e).
What does this mean?
Simply, it is why the derivative of (e)^x = (e)^x, which as we mentioned in the introduction, was one of the fundamental and profound properties of e. And this property occurs because (e) is a ratio, if you stretch the sphere, the cube necessarily stretches such that the ratio of volumes remains constant, (e).

When we consider the derivative of a sphere, where you add an infinitely small amount to the radius, then the volume increases by an infinitely small amount, its surface area.
Two important properties emerge from this stretching of the sphere by its surface area, and the related stretching of the enclosed cube.

Firstly, if you continue to increase the volume, it always increases from its existing size, which is continuously changing, growing bigger by its surface area. And it is this continuous growth of growth that allows it to be used for compound interest (and many other things). This is mathematically represented by (e)^x.

Secondly, because the ratio of the volume of the sphere over its cube is constant (e) for any size sphere, then we know that when we stretch a sphere, the cube will stretch such that their ratio remains (e). i.e. the derivative of the sphere over the derivative cube must maintain the same ratio (e)

Mathematically this is obvious, where (e)^x represents stretching the sphere and thus the cube, and comparing their ratio as they are stretching / changing, their derivatives.

Vs / Vc = (e)L³ / L³ = (e)

Derivative of Vs / Vc = (e)3L² / 3L² = (e)

Basically, because the length terms L cancel, you always get (e) = (e), and this is true if we consider (e)^x, when you raise the above equations to the exponent x, then you simply get (e)^x = (e)^x and the derivative of (e)^x = (e)^x.

Thus we provide a physical geometric meaning, the stretching of a sphere, to why the derivative of (e)^x = (e)^x, explaining this profound property of Euler's e in terms of geometric (e).

Let us now consider area and its derivative, circumference, compared in terms of (e) and L, Pi and r. Again we find these same simple remarkable relationships, as the table below shows.

Object	Cube (e,L)	Ratio	Sphere (Pi,r)	L=1, r=√3/2	r=1, L=2/√3
Area of Circle	√3/2(e)L2	=	Pi r2	√3/2 (e)	Pi
Area of Side of Cube	L2	=	4/3 r2	1	(2/√3)2
Ratio	√3/2 (e)	=	√3/2 (e)	√3/2 (e)	√3/2 (e)
Derivative Area of Circle (Circumference C)	√3(e)L	* Pi/(e) =	2 Pi r	√3(e)	2 Pi
Derivative Area of Side of Cube	2L	* Pi/(e) =	8/3 r	2	8/3
Ratio Derivative	√3/2 (e)	=	√3/2 (e)	√3/2 (e)	√3/2 (e)

As the two colored rows show, the difference to the first table (working with volume) is that when working with area we need to scale (e) by √3/2.

We can now summarize the main relationship, from which we can deduce all other relationships.

√3/2 = (e)/Pi = r/L

From this we see that;

(e) = √3/2 Pi = r/L Pi = Vs/Vc = derivative Vs/Vc = C/2L

Circumference C = 2 Pi r = 2 (e) L

A 180 degree rotation = C/2 = Pi r = (e) L (and e^{i Pi} in Euler's equation)

Volume of Sphere Vs = 4/3 Pi r³ = (e)L³

Euler's Equation, Schrodinger and Waves

Let us consider Euler's famous equation, e^ix = cos x + i sin x.

To explain this equation, consider the diagram, which explains the foundations of trigonometry and Euler's equation.

We see the diagonal length D of a rectangle is enclosed within a unit circle such that the diagonal = hypotenuse = radius = 1.
This allows us to connect the geometry of a right triangle (Pythagoras theorem and the lengths of the sides of the triangle, sin x and cosx), with the geometry of a unit circle (the angle of rotation x of the radius relates to the distance traveled around the circumference in radians).

Euler's equation is then simply showing us two equivalent ways to define points on a circle / rotation around a circle.

The left side, the exponential function e^ix, represents the rotation of the arrow by the angle x (in radians, which is distance traveled around the circle in terms of radius length).

The right side, the complex trigonometric function cos x + i sin x represents a right triangle with sides cos x and sin x, and hypotenuse = radius = 1.
It is a complex function, the imaginary number i simply means a 90 degree rotation, so sin x is rotated 90 degrees to cos x.
The point of the triangle corresponds with the rotated arrow of the exponential function, showing they are equal.

However, it is a deep mathematical mystery as to why we use the number e to represent rotation on a unit circle (where the length of the rotating arrow is 1). I think the reason for this is because (e) can be related to both rotation around the circumference, and to the volume, as we wrote above;

A 180 degree rotation = C/2 = Pi r = (e) L (and e^{i Pi} in Euler's equation)
The volume of a sphere = 4/3 Pi r³ = (e)L³.
And when r = √3/2 then L = 1, thus;

(e) = 180 degree rotation = volume of the sphere.

Significantly, Schrodinger used the exponential function e^i(kx−ωt) in his famous wave equation as a wave operator that generates rotating waves to explain the discrete energy states of light and matter. I discuss this more below, but it relates to the spherical standing wave structure of matter (that creates a 'particle'effect), and the rotating phase waves that naturally occur, so there is this deep connection between the volume of the sphere and the distance around its circumference, that both directly relate to (e).

So let us now look more closely at Euler's equation.

e^ix = cos x + i sin x

When we consider the right hand side in terms of sin waves, then this equation also represents the resultant of two orthogonal plane waves 90 degrees out of phase. i.e.

Cos and sin are 90 degrees out of phase.

The imaginary number i represents a rotation of the sin wave by 90 degrees (orthogonal).

On the internet this is shown using two orthogonal transverse sin waves generating a circular pattern, but this is also true if you use two orthoganal longitudinal plane waves (the wave vibrates forward and back as a compression wave, rather than side to side).

I don't think anyone else has realised this, yet it seemed obvious to me, perhaps because I had been studying Schrodinger's equation, and how Dirac factorised it into three orthoganal plane waves using three imaginary numbers (and very important, as it is a mathematics very similar to quaternions, which are designed for describing a three dimensional reality).

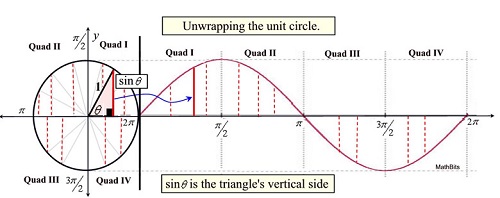
So we have Euler's equation representing two orthoganl plane waves 90 degrees out of phase, creating a resultant phase wave that rotates in a circle.

And now we are led to another profound consideration.

As with the transformation of Pi to three dimensions to deduce (e), we can likewise transform Euler's equation into three dimensions by adding a third orthoganal plane wave, and considering the resultant phase wave in 3 dimensions, as a cubic standing wave with a spherically rotating phase wave (rotate your hand in a circle in front of you, while also moving it forward and back, it forms a spiraling spinor pattern).
We can then transform this cubic geometry to spherical geometry using (e), and thus consider a spherical standing wave and its associated rotating / spiraling phase wave (that seems to explain both the electron and its spin).

 

 

To be completed ...

 

+++++++

 

 

Pythagoras Theorem tells us that cos²x + sin²x = 1
When we factorize this we get;

(cos x + i sin x) (cos x - i sin x) = 1
and
(sin x + i cos x) (sin x - i cos x) = 1

This shows a deep relationship between Euler's equation and Pythagoras equation, and thus suggests a geometric / wave foundation for e.

This is also similar to how Dirac factorized Schrodinger's equation using 3 imaginary numbers, in so doing Dirac re-discovered complex quaternions (Hamilton, Clifford) which represent 3 orthogonal planes, and led to his prediction of electron spin and the existence of the positron.
Thus it is reasonable to conclude that the electron spin is related to the interaction of orthogonal plane waves which cause space to vibrate in circular / spiral patterns (spinors).

Further, since both factors can be either positive or negative, (negative times negative = positive) thus the positron, with its negative sign in the Dirac equation, is not negative energy (as Dirac thought), nor negative time (Feynman's view that the positron is an electron moving backwards in time!), but rather, the negative sign represents the opposite phase spherical standing wave to the electron standing wave. Thus the annihilation of a positron and electron is simply the destructive wave interference of two opposite phase standing waves.

 

Infinitesimal Calculus, Derivatives and Natural Logs

The concept of infinity is very important, since it relates to the validity of the infinitesimal calculus used to calculate e, to represent its continuous change with an infinite sum of discrete changes. I suspect that its very precise solution gives us a sense of certainty, when in fact we have a very precise approximation! (more on this below).

Euler's e is calculated using a Taylor series where;

"The Taylor series of a function is an infinite sum of terms that are expressed in terms of the function's derivatives at a single point. ... the function and the sum of its Taylor series are equal near this point."

 

This summing of derivatives is central to the unique property of e, where the derivative e^x = e^x.

Since mathematics likes to work with discrete things (numbers) it must resort to infinitesimal calculus to calculate e, which converts a discrete relationship (interest added at the end of a unit of time) to a continuous relationship (continuously compounded interest) by using an infinite sum of discrete derivatives and their derivatives ... (Taylor series). i.e If you add an infinite number of infinitely small changes together you get the total.

However, geometric (e), as the ratio of the volume of a sphere to the cube it encloses, is a continuous (and universal) relationship, it applies to all spheres and their enclosed cubes.

And this then allows us to deduce why this summation of derivatives is used to calculate e.
The volume of a sphere can be calculated as the sum of an infinite number of surface areas, each infinitesimally different in size. And we know the derivative of the sphere is the surface area, thus we deduce that the sum of the derivatives of a sphere will equal the volume of the sphere, which equals (e) for r = √3/2, L = 1.

 

It makes much more sense to use the geometric (e), which I suspect is converting from plane waves in two dimensions to three dimensions, from the geometry of cubes to the geometry of spheres.
I believe this relates to physical reality, where the electron and positron can be understood as two opposite phase spherical standing waves (from this foundation mathematical physicist Milo Wolff deduced the de Broglie wavelength and relativistic mass increase due to Doppler shifts of two spherical standing waves in relative motion to one another, thus, for the first time, uniting these fundamentals of quantum physics and special relativity).

 

Interestingly, the only reference I found for the geometric (e) on the internet, was for the ratio of the surface area of a sphere to the surface area of the inscribed tetrahedron (triangular pyramid), which also equals (e).

 

There is much more to write up, much that I do not fully understand. I hope that others can help untangle this fascinating mathematics and its relationship to physical reality.
Please feel free to contact me on Facebook.

Geoff Haselhurst
https://www.facebook.com/geoffrey.haselhurst

4th August, 2017 (Updated 1st October, 2022)

 

Help Humanity

"You must be the change you wish to see in the world."
(Mohandas Gandhi)

"When forced to summarize the general theory of relativity in one sentence: Time and space and gravitation have no separate existence from matter. ... Physical objects are not in space, but these objects are spatially extended. In this way the concept 'empty space' loses its meaning. ... The particle can only appear as a limited region in space in which the field strength or the energy density are particularly high. ...
The free, unhampered exchange of ideas and scientific conclusions is necessary for the sound development of science, as it is in all spheres of cultural life. ... We must not conceal from ourselves that no improvement in the present depressing situation is possible without a severe struggle; for the handful of those who are really determined to do something is minute in comparison with the mass of the lukewarm and the misguided. ...
Humanity is going to need a substantially new way of thinking if it is to survive!" (Albert Einstein)

We can now deduce the most simple science theory of reality - the wave structure of matter in space. By understanding how we and everything around us are interconnected in Space we can then deduce solutions to the fundamental problems of human knowledge in physics, philosophy, metaphysics, theology, education, health, evolution and ecology, politics and society.

This is the profound new way of thinking that Einstein realised, that we exist as spatially extended structures of the universe - the discrete and separate body an illusion. This simply confirms the intuitions of the ancient philosophers and mystics.

Given the current censorship in physics / philosophy of science journals (based on the standard model of particle physics / big bang cosmology) the internet is the best hope for getting new knowledge known to the world. But that depends on you, the people who care about science and society, realise the importance of truth and reality.

It is Easy to Help!

Just click on the Social Network links at top of page, or copy a nice image or quote you like and share it. We have a wonderful collection of knowledge from the greatest minds in human history, so people will appreciate your contributions. In doing this you will help a new generation of scientists see that there is a simple sensible explanation of physical reality (One Substance, One Law) - the source of truth and wisdom, the only cure for the madness of man! Thanks! Geoff Haselhurst (Updated May, 2025)

A new scientific truth does not triumph by convincing its opponents and making them see the light, but rather because its opponents eventually die, and a new generation grows up that is familiar with it. (Max Planck, 1920)

"All that is necessary for evil to succeed is for good people to do nothing."
(Edmund Burke)

"In a time of universal deceit - telling the truth is a revolutionary act."
(George Orwell)

"Hell is Truth Seen Too Late."
(Thomas Hobbes)

---

---

---

---

On Truth & Reality The Spherical Standing Wave Structure of Matter (WSM) in Space
Deducing Most Simple Science Theory of Reality	Metaphysics of Space, Dynamic Unity of Reality	Maths Physics On Mathematics Logic & Reality
Albert Einstein's Special & General Relativity Theory	Quantum Physics Wave Theory of Light & Matter	WSM Cosmology Finite Universe & Infinite Space
Philosophy Wisdom from Truth & Reality	Theology God Religion Spirit Morality	Life Evolution Ecology Nature Environment
Human Health Nutrition Diet Medicine Drugs	Education On Teaching Truth & Reality	Politics Utopia True Democracy Political Science

---

---