---

The Wave Structure of Matter (WSM)
One Substance - One Law - One Logic

---

"Behind it all is surely an idea so simple, so beautiful, that when we grasp it we will all say to each other, how could it have been otherwise? How could we have been so stupid?" (Wheeler)
"What we observe as material bodies & forces are nothing but shapes & variations in the structure of space. Subject & object are one." (Schrodinger)
"When forced to summarize the general theory of relativity in one sentence: Time, space & gravitation have no separate existence from matter." (Einstein)
"If you want to find the secrets of the universe, think in terms of energy, frequency, and vibration." (Tesla)

---

---

---

---

Werner Heisenberg: Uncertainty Principle
Explaining Heisenberg's Uncertainty Principle with the Wave Structure of Matter

The world thus appears as a complicated tissue of events, in which connections of different kinds alternate or overlap or combine and thereby determine the texture of the whole. (Heisenberg, Physics and Philosophy, 1963)

---

Explaining Werner Heisenberg's Uncertainty Principle with the Wave Structure of Matter

I have added below three short deductions / explanations of Heisenberg's Uncertainty Principle from Wave theorists, Mike Harney, Milo Wolff, and Chris Hawkings. The significant point of this is that by removing the 'particle' conception of matter and replacing this with the Wave Structure of Matter we can deduce the Uncertainty Principle due to the spatially extended wave nature of matter. The confusion and paradox of Quantum Theory results from the incorrect discrete 'particle' conception of matter. As Hawking writes;

But maybe that is our mistake: maybe there are no particle positions and velocities, but only waves. It is just that we try to fit the waves to our preconceived ideas of positions and velocities. The resulting mismatch is the cause of the apparent unpredictability. (Hawking, 1988)

Geoff Haselhurst

---

Heisenberg's Uncertainty Principle Derived From Standing Matter Wave Theory

by Michael Harney, June 10, 2005

The following is a derivation of Heisenberg's uncertainty principle based on the discrete nature of standing matter-waves. It will be shown that the uncertainty principle is simply due the quantization of matter based on the discrete nature of standing waves which can only have frequencies that are integer multiples of a fundamental harmonic frequency. This discrete nature leads to a lack of the existence of matter in the domain where n is not an integer because there are no standing waves present when n is fractional, and this has been misinterpreted as uncertainty in measurement.

First we assume standing matter waves which start with fundamental wavelength R equal to the Compton wavelength of the electron, R = 2.4 x 10^-12 meters. Then all other standing waves have wavelengths as follows:

l = R/n , (1)

where n is the quantum number governing the number of nodes in the standing wave. Also, the energy in the standing wave is found from the solution to Schrodinger's equation for a two-dimensional wave trapped in an infinite-potential well:

E = [(n_x)² + (n_y)² ]p²h²/(8mR²), (2)

Where E is the energy in the wave, n_{x and} n_y are the quantum numbers governing the nodes in the two-dimensional wave, and m is the mass of the 'particle' or wave center represented by the fundamental wavelength (when n_{x and} n_y are equal to 1). The mass m for the fundamental wavelength can be found by setting the quantized energy of the fundamental wavelength (using equation 2, setting n = 1) equal to the rest-energy of the 'particle' or wave-center that is represented by this fundamental wavelength:

2p²h²/(8mR²) = mc² (3a)

Solving, we find m = 7.2 x 10^-31 Kg, which is very close to the measured electron mass of 9.11 x 10^-31 Kg.

If we now picture the standing wave of particular quantum numbers n_{x and} n_y we assign n_eff as the square root of the sum of the squares of the n_{x and} n_y so that n_eff represents the effective quantum number, or a composite of n_{x and} n_y. Then we know that when the standing wave changes its quantum numbers n_{x and} n_y by 1, it will effectively change n_eff by one and this is described as D n_eff, the change in effective quantum number either up or down by 1. Then equation 2 above produces an incremental change in energy, D E, for an incremental change in n_eff (which is D n_eff) results in the following:

D E = (D n_eff)² p²h²/(8mR²), (3)

Time is what we perceive from the flow of matter, and therefore from the change in matter waves. As matter waves change incrementally in n_eff (D n_eff), not only does their energy change, but so does their wavelength from the formula:

l = R/n

The change in l with respect to n, which we denote as D l is found by differentiating the l formula (1) above with respect to n_eff to produce:

D l = 2 R/(D n_eff)² , (4)

As l varies (D l) we find that the perception of time also varies based on

D t = D l /c , (5)

where c is the speed of light and the speed at which the matter wave propagates through the space-fabric. Now, based on an incremental change in effective quantum number (D n_eff) which produces an incremental change in energy (D E) and an incremental change in wavelength (D l) which also produces an incremental time shift (D t), we ask the question, what is the minimum product of change in energy (D E) and perceived change in time (or time shift of matter wave, D t)? It is known as (D E)(D t) which will be recognized as Heisenberg's uncertainty relationship. When we substitute the formulas (3), (4), and (5) above in for (D E)(D t) we get:

(D E)(D t) = [(D n_eff)² p²h²/(8mR²)][ 2 R / (c(D n_eff)²)]

which reduces to

(D E)(D t) = p²h²/[4mRc]

where h = Planck's constant, m = 7.2 x 10^-31 Kg, R = 2.4 x 10^-12 meters, and c = 3 x 10⁸ meters/sec. This then evaluates to,

(D E)(D t) = p²h²/[4mRc] = 2.1 x 10^-33 J-sec = approx. h

which is three-times the measured value of Planck's constant (less than order of magnitude).

This shows that an increase in energy which is due to an increasing n (equation 2, which also shows an increase in mass, equation 3a), causes a decrease in D t (eqs. 4 and 5 combined), which makes (D E)D t constant. Therefore, Heisenberg's uncertainty principle is derived from assuming a standing wave formula for all masses (with n = 1 corresponding to l = R = electron matter-wavelength) and applying Schrodinger's equation to calculate the energies in the standing waves.

Heisenberg's uncertainty principle is not a probability function as previously interpreted, but a limit on how much energy and perceived time shift is changed when quantum number n is changed incrementally. It is incorrect to say that we cannot measure energy and time within certain limits (or momentum and distance within certain limits). It is more accurate to say that the standing wave function does not exist in between incremental changes of quantum numbers, and that there is no wave function valid for fractional quantum numbers. For example, going from n = 300 to n = 301 is a valid change in the energy and time displacement of the standing wave function, but there is no measurement possible for n = 300.5 because the standing wave function is not valid in this respect. Therefore, measurement of the function does not and cannot occur. But there would be nothing to measure if we could go to this level - there is no way for the standing matter wave to exist at n = 300.5. Heisenberg's uncertainty principle is merely a limit on the nature of standing waves based on integer quantum numbers. We perceive this to be the limits of what we can measure, but it is only what can really exist.

---

The Uncertainty Principle
You can't have it both ways!

(Milo Wolff, Exploring the Physics of the Unknown Universe, 1994)

Early in the history of Quantum Mechanics, Werner Heisenberg proposed a principle which states limitations on the accuracy of physical measurements. He stated that Nature imposes a minimum value, Plank's constant h, for the product of the errors when measuring position, Dx, and momentum, Dp, when both are measured together. The is usually written

Dx Dp = h

This idea created a great deal of controversy, since it says that nothing is certain - there is always an error in measurements today and these errors will grow larger tomorrow. His principle expanded into discussions of the nature of destiny, religion, and determinism. The philosophers had speculation sessions for decades!

In hindsight his principle is not mystical but obvious to anyone who studies the properties of waves since it has turned out that the principle is a simple property of a wave train and not dependent on QM. It works as follows:

Suppose we have drawings of two wave trains, a) and b) as in Figure 9-6. The length Dx, of the train at a) is long and it's dominant wavelength l can be accurately measured because there are lots of nodes to use. The length of the train at b) is short and the few nodes mean that the dominant wavelength l can be determined only poorly. It is clear that: if the train size is small, the error of wavelength is large. This fact can be put into mathematical terms,

error of wavelength = Dl / l = 1/(number of nodes), and

the number of nodes = the train length / wavelength = Dx / Dl

Put these two equations together and get;

Dx Dl = l² (9-4)

which says the same as the sentence above. i.e. the product of the two errors is a constant, l².

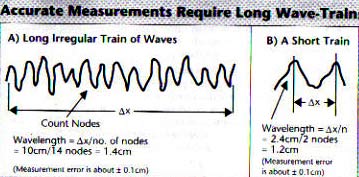
Fig. 9-6 Errors of measuring wavelength
If you wish to accurately measure the wavelength contained in a train of waves, you need to have a large number of nodes to count. The more the nodes the more accurate is the measurement. Thus the accuracy of measuring the long wave-train at (A) is about ten times better than at (B). This fact can be used to demonstrate the truth of the Heisenberg Uncertainty Principle Dx Dp = h

This result can be easily translated into the Heisenberg Uncertainty Principle because of two relations:
1) Dx is the same as the error of position of a particle in the wave.
2) The wavelength is related to particle momentum through the de Broglie relation l=h/p. Switch the l variable into the momentum p, by using the calculus of Chapter 2 to find,

Dl = Dp l²/h

Substitute this into Equation (9-4) to get Dx Dp = h, the Heisenberg Principle. This is what we wanted to prove.

There is another version of the Uncertainty Principle which says that the product of error of time Dt, and the error of energy DE, is also equal to Plank's constant, or

Dt DE = h

You have probably already guessed that this one can be obtained from Equation (9-4) too, by using the relation E = hf. Correct guess.

The uncertainty principle states that if you know the momentum of a particle perfectly, then you can have no knowledge at all of the position. This is because a perfect momentum measurement implies an infinitely long wave, so the particle could be anywhere. Similarly, if the energy is exact, you can have no knowledge of the time when it got there.

The philosophical consequences of this principle depend on whether or not you believe there is actually a 'point particle' somewhere inside the quantum wave. If you say 'yes' then the conclusion must be that Nature, via Quantum Mechanics, imposes a fuzziness on our ability to determine the location of otherwise precise points. If you say 'no' then the conclusion is that the wave packet itself is the 'particle', sometimes smaller, sometimes larger. Then the fuzziness is the character of the 'particle' (as a spherical standing wave), not our ability to find it.

There is one final important difference between the quantum waves and the more familiar light or water waves. It turns out you must often use complex numbers for the wave functions Y. When working with ordinary waves, the complex numbers make the algebra easier. Then when you are done you can go back to real numbers by taking the real part. But for mysterious reasons, the complex numbers are often necessary in QED to get the right answers. No one knows why.

---

Uncertainty Relations and Onion Skin Layering

By Chris Hawkings

From article at https://www.spaceandmotion.com/chris-hawkings-wave-theory.htm

Figure 1

Impression of a typical particle in cross section, showing shells
of high electromagnetic energy density surrounding a central core.

The radial fall-off of the wave's energy density ensures that the particle has no well defined boundary, as shown in figure 1. This poses the difficulty of establishing when a particle is completely detected. Clearly, a particle's detection cannot occur unless its source/sink is absorbed; we take this as the definition of particle detection.

From figure 4, the source/sink is confined to the region of the central core. Thus, particle absorption (source/sink absorption) is assured only with the complete arrival of the central core. For this to occur, the time, , during which the detector is switched on must equal or exceed the time, , it takes for the central core to arrive at the detector (i.e. ). The longitudinal width of the central core is given by and is related to and the group speed, , by . Using these three expressions and , we obtain

      (23)

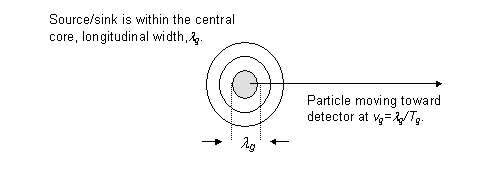
Figure 4
Detector must be on for a time, Dt, greater than the time, T_g, of total reception of the central core at the detector (i.e. Dt³T_g). The distance of flight, Dz, of the central core must exceed the width, l_g, during reception of the central core at the detector (i.e. Dz³l_g).

The distance, , over which the particle travels while the detector is on must also equal or exceed the core width, , if absorption is to be assured (i.e. ). Thus,

      (24)

Pinpointing the source/sink might be regarded as certain to within the half-width of the central core, in which case the right-hand-side of (23) and (24) becomes . In either case, both the formalism and interpretation here are similar to those of the uncertainty relations.

In accordance with this principle, at rest is zero and is undefined, as expected. There is, however, one significant difference. At rest, is , placing an upper limit on equal to the Compton wavelength, . In other words, the source/sink at rest cannot be located within a region, in absolute terms, smaller than this value. This is because smaller sizes would not include the entire central core. Heisenberg's principle, of course, places no such limit, upper or lower, on . This may allow the Compton wavelength to serve as the standard way of expressing the size of all particles at rest. For the proton, this value is 1.321 fm.

Results of p-p scattering at 90^o found by Akerlof (1966) [12] reveal, for the proton, a central core of radius 0.33 fm and two outer shells at 0.50 fm and 0.92 fm from the centre. The spherical shells predicted by equation (5) are found by maximising . These maxima/minima occur (due to the factor) at , where is an integer. Using the Compton wavelength, 1.321 fm, and enumerating for 1, 2 and 3 yields 0.329 fm, 0.659 fm and 0.898 fm. Although a number of interpretations for the scattering results are possible, the correlation between measured values and those predicted by equation (5) are surprisingly consistent, especially considering that the amplitude function played no role in the calculations. Radial fall-off might explain non-detection of further layers beyond . Electron scattering experiments suggest a picture of the electron that is more akin to a 'fuzzy' point particle and which does not appear to possess the onion skin layering typical of the proton. This is not inconsistent with a particle of very small 'rest mass' (long Compton wavelength), whose energy density distribution is similar to that of figure 1. In this instance, the broad central core and shells of low energy density could readily account for the poor definition, point-like appearance and non-detection of onion skin layering.

(Note from Geoff Haselhurst - The figures in this final article from Chris Hawkings are images, as this is how I formatted his full article. See https://www.spaceandmotion.com/chris-hawkings-wave-theory.htm)

---

Heisenberg's Uncertainty Principle
Philosophical / Metaphysical Comments

by Geoff Haselhurst

The following thoughts seem to me to be direct consequences of the Metaphysics of Space and the Wave Structure of Matter.

1. There is no discrete particle thus it is impossible to locate the exact position of something that does not exist (the continuous motion of a 'particle').

2. Motion only applies to the Wave Motion of Space, not the Motion of 'Particles' (or motion of matter in general, as Space is the only existent) thus it is impossible to know the exact momentum of a particle as neither 'particles' or particle velocity (and thus momentum) exist. They are mathematical constructions, and only approximate the real Wave Structure of Matter. Matter actually 'moves' in discrete steps as successive Spherical In-Waves meet at their Wave-Center in discrete locations in Space. So it turns out that Einstein was correct, as he writes;

Thus the last and most successful creation of theoretical physics, namely quantum mechanics (QM), differs fundamentally from both Newton's mechanics, and Maxwell's e-m field. For the quantities which figure in QM's laws make no claim to describe physical reality itself, but only probabilities of the occurrence of a physical reality that we have in view. … I cannot but confess that I attach only a transitory importance to this interpretation. I still believe in the possibility of a model of reality - that is to say, of a theory which represents things themselves and not merely the probability of their occurrence. On the other hand, it seems to me certain that we must give up the idea of complete localization of the particle in a theoretical model. This seems to me the permanent upshot of Heisenberg's principle of uncertainty. (Albert Einstein, 1954)

A few further thoughts;

3. It seems to me that Schrodinger's Equations are founded on de Broglie Matter Waves.
Therefore, Schrodinger equations are not fundamental (as de Broglie waves are Doppler effect / phase wave of two relatively moving spherical (ellipsoidal) standing waves - the real cause of matter and its interactions).
Then I read that Dirac effectively divided Schrodinger's equations into two parts (Milo Wolff has a good section on this in his book) - which according to my logic above is correct (though he did it by chance). Thus I am thinking that wherever you use de Broglie waves, you should really substitute in the real wave equations for two spherical standing waves with relative motion which deduce the de Broglie waves. Does this make sense, is it possible?

4. Problems with Wave Velocity not being Constant
In modern physics the velocity of light c is treated as a constant, rather than (I think) being dependent on wave amplitude (charge) and mass-energy density (gravitational mass). I also think though, that due to wavelength changes with wave velocity the velocity of light is always measured to be the same (a subtle but important difference from being constant, which is a theoretical interpretation of the empirical fact that the velocity is measured to be the same).
Further, the de Broglie wave is a phase wave, caused by matter wave interactions, and has a phase velocity of c²/v where v is the relative velocity. Thus you are effectively working with two different velocity waves.

It is interesting too that when you substitute this phase wave velocity into the energy = frequency equation for matter you get the de Broglie equations, i.e. We first deduce Compton wavelength by relating frequency of matter to energy of matter (as you know)

E = hf = mc², and c = f l,
hc/l = mc²
Thus Compton Wavelength l = h/mc

We can then recalculate above for de Broglie phase wave velocity c²/v = f l, where v is group velocity which I assume is same as apparent velocity of 'particle'.

E = hf = mc², and c²/v = f l,
hc²/vl = mc²
Thus de Broglie Wavelength l = h/mv

This seems to confirm the correctness of the phase wave velocity of de Broglie waves (and is the limit of my maths!, is it correct). Any thought on this? Thanks.
Geoff

---

Mike Harney writes;

Dear Geoff,

Thanks again for the interesting read on the uncertainty from yourself, Milo Wolff and Chris Hawkings. It seems like we all find an easy explanation if we talk about matter waves as opposed to particles. How can a particle be in two places at the same time? It can't - only a wave can do this. Also, I started thinking about Chris' explanation of the onion shells. It does make sense that a proton will have more shells and an electron is fuzzy. The electron with fundamental wavelength (n=1) will have one very indiscrete shell and the proton with n = 1734 with many shells is consistent with this effect.

Schrodinger's equation relates a wave (it's our assumption that it's de Broglie waves, and it appears to be a good one) to time and space displacement. The equation itself is fundamental - there is as of yet no way to reproduce Schrodinger's equation based on WSM that I have seen (as there is as of yet nothing I have seen that describes Maxwell's equations in terms of standing wave theory - it's probably possible but nobody has found it to my knowledge). If you do see Maxwell's equations in terms of spherical standing waves please let me know - it does sound intuitive but I have yet to see formulas. I believe the combination of the uncertainty principle and the fact that Schrodinger's equation is a wave equation pretty much describes all of quantum mechanics in terms of WSM. But the key is getting away from probability and uncertainty - this is how I think the uncertainty principle relates to standing matter waves. The derivation (above) does show a pretty good match to Planck's constant - more than a coincidence!

The one thing that still comes back to me is that as there are standing matter waves that create our masses, the waves must be undergoing compression and tension in this fabric. The nature of the compressibility of this fabric is what truly interests me because I believe it is the key to how the waves interact and this in turn governs all of our universal constants. Also, the question of the what is the fabric and what makes it compressible is exciting - how does this really occur? We don't believe in a mystical nature for waves (tossing out the Born interpretation of Schrodinger) so it must still be a fabric in compression or tension in order for wavelengths to shift, for wave-centers to be elongated, etc. This is all just classical wave mechanics which means space really behaves like a material, a continuous medium of some sort.
I think this may be the solution to what Milo is looking for in relating WSM to nuclear fusion.

Equations show this relationship between the strong-nuclear interaction and it's range. I believe the short range of the strong nuclear force is due to being on the "knee" of the elastic-potential energy curve for the fabric of space. Once we understand how this works, controlling it should be much easier. It's also interesting that the Newtonian force law of 1/r² which is so prevalent in keeping field theory alive is really just proportional to an x-displacement squared (kx²) and this is more accurate for explaining interaction of waves from very large distances to very small. Thus, the field concept is keeping theorists from uniting gravity (even General Relativity's version of gravity) with nuclear interactions. No wonder they are frustrated - the 1/r² breaks down very quickly at small r (hell - it becomes a singularity!). No way to do it with the continuous field concept - they must adapt wave interaction and compressibility of space.
Thanks for the interesting articles.
Mike Harney

Help Humanity

"You must be the change you wish to see in the world."
(Mohandas Gandhi)

"When forced to summarize the general theory of relativity in one sentence: Time and space and gravitation have no separate existence from matter. ... Physical objects are not in space, but these objects are spatially extended. In this way the concept 'empty space' loses its meaning. ... The particle can only appear as a limited region in space in which the field strength or the energy density are particularly high. ...
The free, unhampered exchange of ideas and scientific conclusions is necessary for the sound development of science, as it is in all spheres of cultural life. ... We must not conceal from ourselves that no improvement in the present depressing situation is possible without a severe struggle; for the handful of those who are really determined to do something is minute in comparison with the mass of the lukewarm and the misguided. ...
Humanity is going to need a substantially new way of thinking if it is to survive!" (Albert Einstein)

We can now deduce the most simple science theory of reality - the wave structure of matter in space. By understanding how we and everything around us are interconnected in Space we can then deduce solutions to the fundamental problems of human knowledge in physics, philosophy, metaphysics, theology, education, health, evolution and ecology, politics and society.

This is the profound new way of thinking that Einstein realised, that we exist as spatially extended structures of the universe - the discrete and separate body an illusion. This simply confirms the intuitions of the ancient philosophers and mystics.

Given the current censorship in physics / philosophy of science journals (based on the standard model of particle physics / big bang cosmology) the internet is the best hope for getting new knowledge known to the world. But that depends on you, the people who care about science and society, realise the importance of truth and reality.

It is Easy to Help!

Just click on the Social Network links at top of page, or copy a nice image or quote you like and share it. We have a wonderful collection of knowledge from the greatest minds in human history, so people will appreciate your contributions. In doing this you will help a new generation of scientists see that there is a simple sensible explanation of physical reality (One Substance, One Law) - the source of truth and wisdom, the only cure for the madness of man! Thanks! Geoff Haselhurst (Updated May, 2025)

A new scientific truth does not triumph by convincing its opponents and making them see the light, but rather because its opponents eventually die, and a new generation grows up that is familiar with it. (Max Planck, 1920)

"All that is necessary for evil to succeed is for good people to do nothing."
(Edmund Burke)

"In a time of universal deceit - telling the truth is a revolutionary act."
(George Orwell)

"Hell is Truth Seen Too Late."
(Thomas Hobbes)

---

---

---

---

On Truth & Reality The Spherical Standing Wave Structure of Matter (WSM) in Space
Deducing Most Simple Science Theory of Reality	Metaphysics of Space, Dynamic Unity of Reality	Maths Physics On Mathematics Logic & Reality
Albert Einstein's Special & General Relativity Theory	Quantum Physics Wave Theory of Light & Matter	WSM Cosmology Finite Universe & Infinite Space
Philosophy Wisdom from Truth & Reality	Theology God Religion Spirit Morality	Life Evolution Ecology Nature Environment
Human Health Nutrition Diet Medicine Drugs	Education On Teaching Truth & Reality	Politics Utopia True Democracy Political Science

---

---